AB: Pythagoras in Körpern
Mit dem Satz des Pythagoras lassen sich diagonale Strecken auf Seitenflächen von geometrischen Körpern berechnen. Die folgenden Aufgaben überprüfen, ob du diese berechnen kannst.
Benutze den Satz des Pythagoras, um die fehlenden Diagonalen zu berechnen.
Berechne die Flächendiagonale d beim Würfel mit Seite a = 5 cm
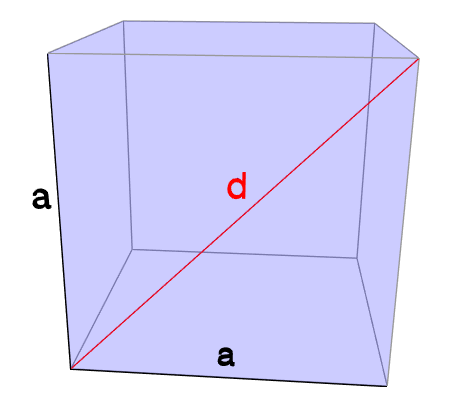
\( a^2 + a^2 = d^2 \\ d = \sqrt{a^2 + a^2} \\ d = \sqrt{(5 \;cm)^2 + (5 \;cm)^2} \\ d = \sqrt{50 \;cm^2} \approx 7,071 \;cm \)
Berechne die Raumdiagonale e beim Würfel mit Seite a = 4 cm

Flächendiagonale \( d = \sqrt{a^2 + a^2} \), damit:
\( e^2 = d^2 + a^2 \)
\( e^2 = (\sqrt{a^2 + a^2})^2 + a^2 \)
\( e^2 = (a^2 + a^2) + a^2 = 3·a^2 \)
\( e = \sqrt{3 · a^2} \)
\( e = \sqrt{3 · (4 \;cm)^2} = \sqrt{48 \;cm^2} \approx 6,928 \;cm \)
Flächendiagonale d beim Quader mit Länge = 4 cm, Breite = 5 cm und Höhe = 3 cm
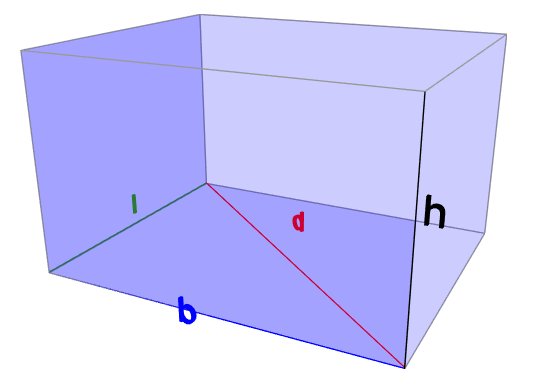
\( d^2 = b^2 + l^2 \\ d = \sqrt{b^2 + l^2} \\ d = \sqrt{(5 \;cm)^2 + (4 \;cm)^2} \\ d = \sqrt{41 \;cm^2} \approx 6,403 \;cm \)
Raumdiagonale e beim Quader mit Länge = 3 cm, Breite = 6 cm und Höhe = 3 cm
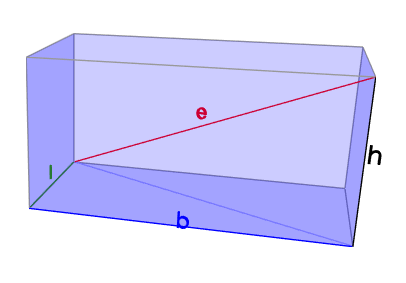
Flächendiagonale \( d = \sqrt{b^2 + l^2} \), damit:
\( e^2 = d^2 + h^2 \)
\( e^2 = (\sqrt{b^2 + l^2})^2 + h^2 \)
\( e = \sqrt{ b^2 + l^2 + h^2 } \)
\( e = \sqrt{ (6\;cm)^2 + (3\;cm)^2 + (3\;cm)^2 } \)
\( e = \sqrt{54 \;cm^2} \approx 7,3485 \;cm \)
Seitenkante s bei der quadratischen Pyramide mit Seite a = 4 cm und Höhe h = 3 cm.
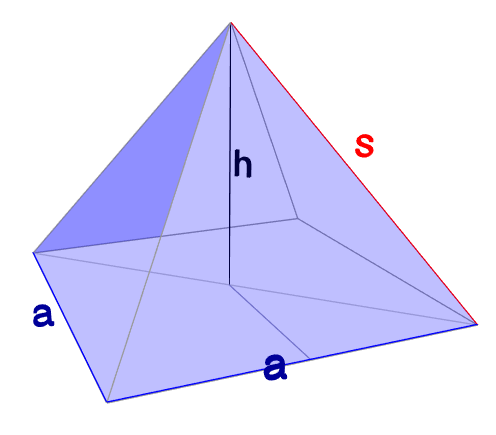
Seitenkante: \( s = \sqrt{ h^2 + \frac{a^2}{2} } \)
\( s = \sqrt{ h^2 + \frac{a^2}{2} } \)
\( s = \sqrt{ (3 \;cm)^2 + \frac{(4 \;cm)^2}{2} } \)
\( s = \sqrt{ 17 \;cm^2 } \approx 4,123 \;cm \)
Flächendiagonale d der Grundfläche der quadratischen Pyramide mit Seite a = 6 cm und Höhe h = 4 cm.

\( d^2 = a^2 + a^2 \\ d = \sqrt{ a^2 + a^2 } = \sqrt{ 2·a^2 } \\ d = \sqrt{ 2·(6 \;cm)^2 } \\ s = \sqrt{ 72 \;cm^2 } \approx 8,485 \;cm \)
