Was sind obere und untere Schranke?
Die obere Schranke ist definiert als: s ≥ f(x), also ein Wert s, der von der Funktion nicht überschritten wird.
Die untere Schranke ist definiert als: s ≤ f(x), also ein Wert s, der von der Funktion nicht unterschritten wird.
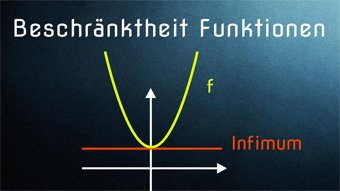
Was sind Supremum und Infimum?
Das Supremum ist die kleinste obere Schranke.
Das Infimum ist die größte untere Schranke.
Oben und unten beschränkte Funktionen
Merke: Eine Funktion ist nach unten beschränkt, wenn es eine Zahl s gibt, die von f(x) nicht unterschritten wird. s ≤ f(x)
Merke: Eine Funktion ist nach oben beschränkt, wenn es eine Zahl s gibt, die von f(x) nicht überschritten wird. s ≥ f(x)

y = 1 ist eine untere Schranke. Sie ist sogar das Infinum, also die größte untere Schranke. Genauso gut hätten wir aber auch y = -4 oder y = -12345 als eine mögliche untere Schranke wählen können. Diese Werte sind „außerhalb“ des Wertebereichs der Funktion.

y = 1 ist eine obere Schranke. Sie ist hier sogar das Supremum, also die kleinste obere Schranke. Genauso gut hätten wir aber auch y = 5 oder y = 5712 als eine mögliche obere Schranke wählen können. Diese Werte sind „innerhalb“ des Wertebereichs der Funktion.
Keine Beschränktheit
Wenn alle möglichen y-Werte angenommen werden (alle reellen Zahlen ℝ), dann hat die Funktion keine Beschränktheit.

Obere und untere Schranke beim Sinusgraph

Obere und untere Schranke beim Intervall

Mehrere Schranken s bei s ≤ f(x)
Durch die Definition der unteren Schranke(n) mit s ≤ f(x) gilt, dass s gleich f(x) sein kann, aber auch Werte kleiner als f(x) annehmen darf. Das heißt, s kann beliebige Werte unter f(x) annehmen. Es gibt also nicht nur eine untere Schranke. Gleiches gilt für die obere Schranke.

Das Infimum s = -4 ist die größte untere Schranke.

Das Supremum s = 4 ist die kleinste obere Schranke.