Eine gerade Funktion ist eine Funktion, die nur gerade Exponenten hat (also alle ganzzahligen Exponenten sind durch 2 teilbar, ohne Rest).
Eine ungerade Funktion ist hingegen eine Funktion, die nur ungerade Exponenten besitzt.
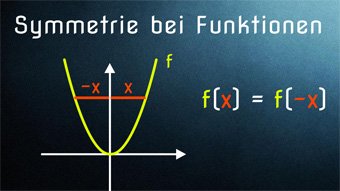
Gerade Funktionen sind stets achsensymmetrisch, zum Beispiel f(x) = x2 oder g(x) = x4 + x2 + x0 = x4 + x2 + 1.
Ungerade Funktionen sind stets punktsymmetrisch, zum Beispiel f(x) = x3 + x.
Die Koeffizienten (also die Zahlen in Multiplikation vor den Variablen, wie 3·x2) beeinflussen die Symmetrieart nicht.
Die Achsensymmetrie kann auch als Spiegelung an der Symmetrieachse verstanden werden. Die Punktsymmetrie kann als 180°-Drehung des Graphen um das Symmetriezentrum verstanden werden.