Kommutativ meint das Vertauschen der einzelnen Zahlen. Das Rechengesetz gilt für Addition und Multiplikation, jedoch nicht für Subtraktion und Division.
Wir nutzen im Folgenden Variablen zur Darstellung der Gesetze. Variablen sind Buchstaben, die anstelle von Zahlen stehen. Wenn wir 3 + 5 = 8 haben, können wir dies mit Variablen schreiben als: a + b = c. Wir wissen dann, dass a=3 und b=5 und c=8.
Bei a + b = c können wir beliebige Zahlen einsetzen, zum Beispiel a=2 und b=4 und damit ergibt sich c=6, also 2 + 4 = 6.
Man nutzt Variablen also, um einen Sachverhalt allgemein darzustellen. Genau dies machen wir hier (wir können uns für a und b jeweils zwei Zahlen wählen und das Rechengesetz so testen):
Für die Addition: a + b = b + a
Für die Multiplikation: a · b = b · a
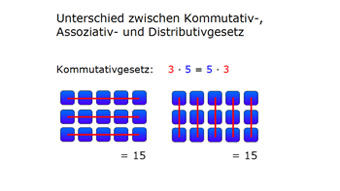
Grafische Darstellung vom Kommutativgesetz


Kommutativgesetz in der Sprache
Das Kommutativgesetz findet man übrigens auch in den Sprachen wieder. Auf Deutsch sprechen wir zum Beispiel die Zahl 49 als "neun und vierzig". Mathematisch geschrieben ist das: 9 und 40, also 9 + 40. Auf Englisch spricht man hingegen die Zahl 49 als „forty-nine“, also 40 + 9. Wie wir sehen, wurde hier das Kommutativgesetz „angewendet“.
Kommutativgesetz für Multiplikation (via Addition)
Ein anschauliches Beispiel, das zeigt, dass das Kommutativgesetz auch für die Multiplikation gilt, also a·b = b·a. Wir zerlegen hierzu die Zahlen in kleinere Zahlen und verwenden das Kommutativgesetz der Addition:
= 3 · 4
= 4 + 4 + 4
= (3+1) + (3+1) + (3+1)
= 3 + 1 + 3 + 1 + 3 + 1
= 3 + 3 + 3 + 1 + 1 + 1
= 3 + 3 + 3 + 3
= 4 · 3
Kommutativgesetz mit drei Variablen
Kommutativgesetz mit drei Variablen für die Addition:
a + b + c =
a + c + b =
b + a + c =
b + c + a =
c + a + b =
c + b + a
Kommutativgesetz mit drei Variablen für die Multiplikation:
a · b · c =
a · c · b =
b · a · c =
b · c · a =
c · a · b =
c · b · a