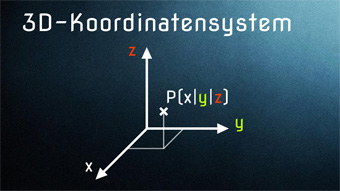
Das Besondere gegenüber der Planimetrie (der ebenen Geometrie), wo wir uns im Zweidimensionalen befinden und unsere Punkte im Koordinatensystem über A(x|y) bestimmt werden, ist, dass wir eine dritte Komponente für die Höhe erhalten.
Ein Punkt im 3D-Koordinatensystem wird also über B(x|y|z) angegeben, wobei z die Höhe darstellt, die auf den Betrachter zuläuft.
Im Folgenden die Draufsicht auf ein 3D-Koordinatensystem:

Da man auf einem zweidimensionalen Blatt Papier Schwierigkeiten hat, eine Höhe „nach oben herauskommen“ zu lassen, wird ein 3D-Koordinatensystem in Schrägansicht dargestellt.

Die folgende Animation zeigt, wie wir von der zweidimensionalen zur dreidimensionalen Darstellung kommen:

Mit einem dreidimensionalen Koordinatensystem und den drei Achsen für x, y und z können wir die Position eines Punktes eindeutig beschreiben. Zum Beispiel liegt A(0|0|0) im Koordinatenursprung.
Mit Punkten lassen sich dann auch Strecken und Körper exakt beschreiben und Berechnungen durchführen.

Die drei Ebenen, die durch die x-, y- und z-Achse aufgespannt werden, teilen den Raum in 8 Abschnitte. Diese Abschnitte nennen wir „Oktanten“ (von lat. „octo“ = acht).