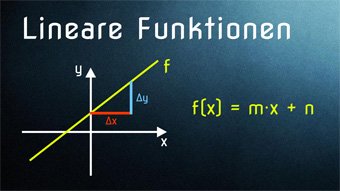
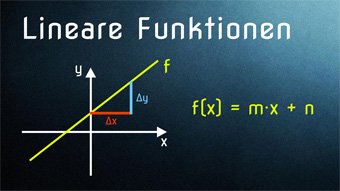
Die Normalform einer linearen Funktion sieht so aus:
f(x) = m·x + n
Dabei entspricht das m der Steigung und das n steht für den y-Achsenabschnitt, es beschreibt also, in welcher Höhe die y-Achse geschnitten wird.
Für f(x) = 2·x + 4 wird die y-Achse in einer Höhe von 4 geschnitten und die Steigung beträgt 2.

Steigung m
Die Steigung m gibt den Verlauf des Funktionsgraphen an. Wir unterscheiden folgende Fälle:
- Ist m positiv, so steigt der Graph stetig.
- Ist m negativ, so fällt der Graph stetig.
- Ist m = 0, dann haben wir eine sogenannte konstante Funktion. Die Gerade ist parallel zur x-Achse.
Zu sehen sind die Fälle auch an den drei folgenden Graphen.

Die Steigung kann dabei als sogenanntes Steigungsdreieck betrachtet werden bzw. mit einem Steigungsdreieck berechnet werden.
Das heißt, wir zeichnen einen Abstand für x (von links nach rechts) und einen Abstand für y (von unten nach oben) ein und berechnen deren Verhältnis per Division.
Der Abstand für x ergibt sich aus einem x-Wert und einem folgenden x-Wert, wir schreiben Differenz Δx = x2 - x1.
Das Δx wird „Delta x“ genannt und meint einfach nur den Abstand zwischen zwei x-werten.
Die Steigung berechnet sich somit über: \( m = \dfrac{y_2 - y_1}{x_2 - x_1} = \frac{ \normalsize{ \Delta y } }{ \normalsize{ \Delta x } } \)
Dies sei beispielhaft an unserer Funktion f(x) = 2·x + 4 gezeigt:

Hier gehen wir mit dem x-Wert um 1 Einheit nach rechts. Die Differenz (das Zeichen Δ steht für Differenz bzw. Abstand) aus x2-x1 ist also 1.
Rechnerisch festgehalten: Δx = x2 - x1 = 1 - 0 = 1.
Nun muss noch die Höhe abgelesen werden. Dazu müssen wir 2 Einheiten nach oben gehen. Die Differenz für y ist Δy = 2. Wir können sie berechnen über Δy = y2 - y1 = 6 - 4 = 2.
Das m ergibt sich dann mit \( m = \dfrac{ \Delta y }{ \Delta x } = \dfrac{2}{1} = 2 \).
y-Achsenabschnitt
Während m die Steigung angibt, gibt der y-Achsenabschnitt n die „Höhe“ der Geraden an, an welcher sie die y-Achse schneidet. Dadurch wird die Gerade also verschoben.

Die drei Geraden haben die gleiche Steigung, sind aber nach oben bzw. unten verschoben. Man spricht hier von „parallelen Geraden“.
Spezialformen wie f(x)=x
Eine lineare Funktion hat die Normalform f(x) = m·x + n. Dies ist manchmal nicht sofort zu erkennen, wenn beispielsweise g(x) = x angegeben ist. Hier haben wir m = 1 und n = 0, also eine lineare Funktion in der Form g(x) = 1·x + 0 vorzuliegen, wobei die 0 und die 1 nicht hingeschrieben wurden.
Dies gilt ebenfalls für die bereits erwähnte konstante Funktion, die keine Steigung hat (also m = 0). Hier wird meist notiert: f(x) = n, als Normalform wäre dies: f(x) = 0·x + n. Der Graph einer konstanten Funktion ist parallel zur x-Achse.

Merken wir uns außerdem: Geht der Graph durch den Koordinatenursprung, so ist n = 0 und aus:
f(x) = m·x + n | n = 0
wird zu:
f(x) = m·x + 0
f(x) = m·x
Oder: Haben wir zum Beispiel die Gleichung: f(x) = x, so wissen wir, dass sie sich ebenfalls in die Normalform bringen lässt: f(x) = 1·x + 0
Wir finden die Normalform auch bei Gleichungen, die keine Steigung haben. So lässt sich z. B. f(x) = 2 auch darstellen als f(x) = 0·x + 2.
Hier gibt es keine Steigung und wir erhalten eine Parallele zur x-Achse, die die y-Achse bei y = 2 schneidet. Solche Funktionen heißen konstante Funktionen.
Winkelhalbierende
Interessant ist noch, dass g(x) = x auch unter dem Namen „1. Winkelhalbierende“ bekannt ist, da sie im ersten Quadranten (also dort wo x und y positiv sind), den Winkel von 90° halbiert und mit 45° verläuft.
Neben der 1. Winkelhalbierenden gibt es noch die „2. Winkelhalbierende“, die von links oben nach rechts unten verläuft, sie hat die Funktionsgleichung h(x) = -x.