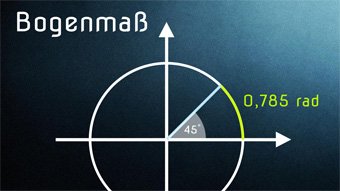
In diesem Artikel lernen wir das Bogenmaß kennen. Es ist neben dem Gradmaß das am häufigsten verwendete Maß, um Winkelgrößen anzugeben.
Bei den Winkelmaßen hatten wir erfahren, dass Winkel auch mit anderen Einheiten angegeben werden können:
- Gradmaß (90°)
- Prozent (25 %)
- Zeitmaß (3 Stunden)
- Gon (100 Gon)
- Bogenmaß (\( \frac{1}{4} \) · Pi)
Gradmaß und Bogenmaß
Beim Gradmaß teilen wir den Kreis in 360 Schritte und legen dann Winkel von 0° bis 360° fest. Beim Bogenmaß hingegen geht es um das Verhältnis vom Kreisbogen zum Radius.
Wenn der Radius r ist und der Kreisbogen b, dann würde man aufstellen Winkel α = b/r. Der Winkel wird als Verhältniswert angegeben mit Bezug auf den Radius. Anders gesagt, wir messen den Winkel mit Hilfe des Radius und des Kreisbogens und nennen es Bogenmaß.
Die Einheit für das Bogenmaß ist “Radiant” und wird mit “rad” abgekürzt. Hier einige Beispiele:
0° = 0 rad
90° ≈ 1,571 rad
180° ≈ 3,142 rad
270° ≈ 4,712 rad
360° ≈ 6,283 rad
Merken wir uns: Egal, welche Größe unser Kreis hat, bei zum Beispiel 90° ist der Kreisbogen immer rund 1,571 mal so groß wie der Radius. Also wenn wir einen Radius von 15 cm hätten, dann wäre der Kreisbogen ≈ 15 cm · 1,571 lang.
Wir können wählen, ob wir den Winkel schreiben als α = 90° oder α ≈ 1,571 rad. Beide Schreibweisen sind korrekt.