Beim Umrechnen mit dem Taschenrechner kann es zu Fehlern kommen, wenn ihr das falsche Winkelmaß eingestellt habt. Beim Taschenrechner gibt es eine „Modus“-Taste (oder MODE), mit der wir das Winkelmaß umstellen können:

Für uns sind die beiden Modi DEG („Degree“, also Grad) und RAD („Radian“, also Radiant) wichtig. Wir müssen beim englischen Taschenrechner übrigens aufpassen: GRAD meint hier „Gon“ (englisch „Gradian“). Das ist die Einteilung des Kreises in 400 Schritte. Für 360° nehmen wir immer DEG.
Bei den Sinuseingaben haben wir bisher fast immer Gradmaß gehabt, also zum Beispiel: sin(90°) = 1.
Wenn wir den Modus auf RAD umstellen, ergibt die Eingabe von sin(90) = 0,89399… also einen anderen Wert, da gerechnet wurde: sin(90 rad).
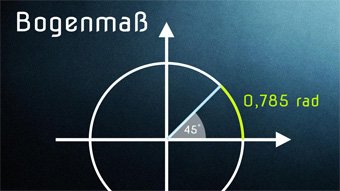
Wenn wir 90° in Bogenmaß eingeben wollen, dann nehmen wir 0,5·π. Damit: sin(0,5·π) ≈ sin(1,5708) ≈ 1.
Wollen wir sin(π) berechnen, also sin(180°), dann tippen wir ein sin(π) = 0.
Wir können testen, ob der Taschenrechner richtig eingestellt ist, indem wir schauen, ob im Display Rad oder Deg steht oder - falls nicht - einfach sin(90) eingeben und schauen, ob 1 herauskommt, denn dann ist es Gradmaß.
Sinusfunktion und Bogenmaß
Bei der Sinusfunktion können wir nun die Winkel anstatt mit Grad auch mit Radiant angeben (siehe x-Achse).

Auch hier können wir die Parameter der allgemeinen Sinusfunktion verändern, wir verschieben den Graphen jetzt nicht um Grad, sondern um π. Von 180° auf 90° ist das Gleiche wie von π auf 0,5 π.
Als nächstes machen wir mit den trigonometrischen Gleichungen weiter. Wir schauen uns an, wie man sin(x) = 0,5 oder 2·cos(x) = -0,5 rechnerisch lösen kann.