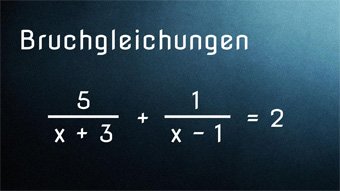Wie gesagt, funktioniert das Lösen von Bruchgleichungen genau wie bei Gleichungen, die wir schon kennen. Vorarbeit muss aber bezüglich der Definitionsmenge getätigt werden. Auch sollte der Nenner entfernt werden, was eine einfachere Bearbeitung der Gleichung erlaubt.
Beispiel einer Bruchgleichung:
\( \frac{1}{x} = 2 \)
Die Definitionsmenge lässt sich hier zu D = ℝ \ {0} bestimmen, das heißt der Wert x = 0 darf nicht angenommen werden.
Um den Nenner zu entfernen wird die Gleichung ganz einfach auf beiden Seiten mit diesem multipliziert:
\( \frac{1}{x} = 2 \quad |· x \\ 1 = 2 · x \quad | :2 \\ x = \frac{1}{2} \)
Da \( x = \frac{1}{2} \) in der Definitionsmenge liegt (in der erlaubten Zahlenmenge), darf die \( \frac{1}{2} \) als Lösung verwendet werden. Sicherheit gibt hier auch eine Probe, also das Einsetzen des x-Wertes in die Bruchgleichung und das Überprüfen auf eine wahre Aussage hin.
Für das Lösen von Bruchgleichungen gibt es verschiedene Verfahren. Das wichtigste ist wohl das Verständnis bezüglich des Hauptnenners. Dieser ist das sogenannte kleinste gemeinsame Vielfache aller Nenner. Ist man nicht in der Lage den Hauptnenner zu finden, kann man sich auch mit einem gemeinsamen Nenner zufrieden geben, also einem beliebigen Vielfachen aller Nenner, man wird aber mit größeren Zahlen arbeiten müssen, was die Rechenarbeit erschweren mag. Wir konzentrieren uns hier also auf den Hauptnenner.
Um den Hauptnenner zu bilden, muss man sich an Brüche erinnern, die wir erweitern und kürzen können. Mit diesen Hilfsmitteln können wir die Hauptnenner erschaffen. Dies sei an einem Beispiel gezeigt.
\( \frac{5}{x+3} + \frac{1}{x-1} = 2 \)
Bevor wir beginnen bestimmen wir noch den Definitionsbereich. Dieser ist hier D = ℝ \ {-3; 1}.
Nun zur Bestimmung des Hauptnenners. Dieser ergibt sich hier aus der Multiplikation beider vorhandener Nenner, sprich (x+3)·(x-1). (Ein beliebiger gemeinsamer Nenner wäre beispielsweise 3·(x+3)·(x-1), soll uns hier aber nicht weiter interessieren.)
Um diesen Hauptnenner nun bei jedem Bruch zu erschaffen, müssen die Brüche entsprechend erweitert werden. Bei dem ersten Bruch muss dazu mit (x-1) multipliziert werden und bei dem zweiten Bruch mit (x+3). Die rechte Seite der Gleichung (dort wo die 2 alleine steht) muss komplett mit dem Hauptnenner erweitert werden. Damit ergibt sich:
\( \frac{5·\textcolor{blue}{(x-1)}}{(x+3)·\textcolor{blue}{(x-1)}} + \frac{1 · \textcolor{blue}{(x+3)}}{(x-1)·\textcolor{blue}{(x+3)}} = \frac{2·\textcolor{blue}{(x+3)·(x-1)}}{\textcolor{blue}{(x+3)·(x-1)}} \)
Tipp: Es muss hierbei der Nenner (x+3)·(x-1) nicht ausmultipliziert werden, denn im nächsten Schritt wird die gesamte Gleichung schlicht mit diesem multipliziert. Wir multiplizieren also den Nenner mit der Gleichung, damit aus der Bruchgleichung eine Gleichung ohne Brüche entsteht:
\( \frac{5·(x-1)}{\textcolor{blue}{(x+3)·(x-1)}} + \frac{1 · (x+3)}{\textcolor{blue}{(x+3)·(x-1)}} = \frac{2·(x+3)·(x-1)}{\textcolor{blue}{(x+3)·(x-1)}} \quad| \textcolor{red}{· (x+3)·(x-1)} \\ 5 · (x-1) + (x+3) = 2·(x+3)·(x-1) \)
Nun wird wie gewohnt ausgerechnet. In diesem Fall müssen wir ausklammern und dann so umformen, dass die p-q-Formel angewendet werden kann.
\( 5·(x-1) + (x+3) = 2·(x+3)·(x-1) \\ 5· x - 5 + x + 3 = 2(x^2-x-3+3· x) \\ 6· x - 2 = 2· x^2 - 2· x - 6 + 6· x \\ 6· x - 2 = 2· x^2 + 4· x - 6\quad|-6· x + 2 \\ 2· x^2 - 2· x - 4 = 0 \quad |:2 \\ x^2 - x - 2 = 0 \\ x^2 + (-1)· x + (-2) = 0 \quad|\text{p-q-Formel} \\ x_{1,2} = -\frac{-1}{2} \pm \sqrt{\left(\frac{-1}{2}\right)^2 + 2} \\ x_{1,2} = \frac{1}{2} \pm \sqrt{\frac{1}{4} + 2} \\ x_{1,2} = \frac{1}{2} \pm \sqrt{\frac{9}{4}} \\ x_{1,2} = \frac{1}{2} \pm \frac{3}{2} \\ x_1 = \frac{1}{2} - \frac{3}{2} = -1 \\ x_2 = \frac{1}{2} + \frac{3}{2} = 2 \)
Diese beiden Lösungen liegen innerhalb der Definitionsmenge und demnach kann die Lösungsmenge als L = {-1; 2} aufgeschrieben werden.
Schema zum Lösen von Bruchgleichungen
Es ergibt sich also folgendes Schema zum Lösen von Bruchgleichungen:
- Definitionsmenge bestimmen
- Erweitern der Brüche auf den Hauptnenner (oder einen gemeinsamen Nenner)
- Gleichung umformen, sodass alle Nenner wegfallen
- Gleichung nach x auflösen
- Ermittelte x-Werte mit der Definitionsmenge vergleichen, Lösungen bestimmen