Wenn wir den Wert der Kreiszahl π herleiten wollen, der 3,1415926535… beträgt, gibt es mehrere Wege hierfür. Wir schauen uns im Folgenden eine Möglichkeit an:
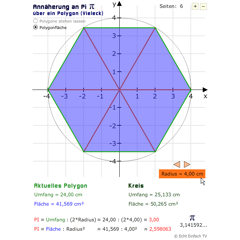
Legen wir als erstes ein regelmäßiges Vieleck in einen Kreis:

Wir wissen, dass der Kreisumfang größer als der Umfang des innenliegenden Quadrates ist. Wenn wir jetzt die Seitenzahl dieses Vielecks erhöhen (zum Beispiel ein Achteck erstellen), so nähert sich der Umfang des Vielecks der Kreislinie an.
Je mehr Seiten wir haben, desto näher kommt der Wert des Umfangs des Vielecks dem Umfang des Kreises.
Mit einer Formel, die den Umfang des Vielecks angibt, können wir uns also dem Wert des Kreisumfangs annähern.
Um die Seitenlängen des Vielecks zu berechnen, verwenden wir den Sinus.
Für den Sinus benötigen wir rechtwinklige Dreiecke, die wir als senkrechte Strecken vom Mittelpunkt zur Seite des Vielecks einzeichnen können. Bei diesen rechtwinkligen Dreiecken können wir Sinus, Kosinus und Tangens anwenden.

Wir sehen, dass es vier gleich große Winkel im dargestellten Viereck gibt. Der für das Dreieck benötigte Winkel entspricht der Hälfte eines Winkels.
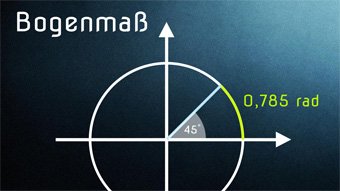
Das heißt wir rechnen 360° durch die Seitenanzahl, also durch 4 und erhalten dann \( \frac{1}{4} \) von 360°. Diesen Wert halbieren wir und kommen somit auf 45°.
Nun können wir den Sinus von dem Winkel α bestimmen mittels Gegenkathete durch Hypotenuse.
Die Hypotenuse ist der Kreisradius und 1 Einheit lang.
Wir wissen, dass uns der Sinus die Länge der Gegenkathete angibt, wir berechnen sin(45°) ≈ 0,707. Das ist die Länge der Vielecks-Seite. Diese Seite haben wir jetzt 8 mal. So erhalten wir den umfang 8 · 0,707 cm = 5,656 cm. Der Kreisumfang muss demnach größer sein als 5,656 cm.
Allgemeine Formel zur Annäherung an den Kreisumfang
Umfang = Seiten·(2·sin(α) · Radius) | Radius = 1
Umfang = n·(2·sin(α) · 1)
Diese Formel lässt sich auf jedes Vieleck (Polygon) anwenden. Um so mehr Seiten wir wählen, desto genauer wird der Wert für Pi. Bei einem 33-Eck haben wir einen Wert von ca. 3,1369 cm (als Annäherung an den Wert von Pi).
Zu beachten bleibt, dass wir den Wert der Zahl Pi jedoch nie erreichen werden, denn sie ist eine irrationale transzendente Zahl. Das heißt, sie hat unendlich viele Nachkommastellen.