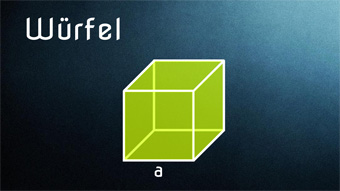
Zur Herleitung der Formel für die Raumdiagonale müssen wir uns zuerst die Flächendiagonale d vor Augen führen, denn diese können wir mit dem Satz des Pythagoras aus zwei Würfelseiten berechnen: d² = a² + a², damit also d = √(a² + a²)

Weiterhin erkennen wir, dass die Raumdiagonale e mit der Diagonale d und einer Seite a ein rechtwinkliges Dreieck aufspannt.

Hier lässt sich ebenfalls der Satz des Pythagoras verwenden und wie folgt aufstellen:
\( e^2 = \sqrt{d^2 + a^2} \)
Wir wissen aus dem Absatz zuvor, dass d = √(a² + a²), setzen wir dies für d² ein.
e² = d² + a²
e = √(d² + a²)
e = √((a²+a²) + a²)
e = √(a² + a² + a²) | a² + a² + a² = 3·a²
e = √(3·a²) | Wurzel auf beide Faktoren ziehen
e = √3·√a²
e = √3·a | oder mit vertauschten Faktoren
e = a·√3
Und schon haben wir die Formel für die Raumdiagonale des Würfels hergeleitet.
e = a·√3