Bevor man die Antiproportionalität behandelt, sollte man die Proportionalität verstanden haben, denn die Antiproportionalität ist die Umkehrung der Proportionalität.
Was ist Antiproportionalität?
Klären wir zunächst, was das Wort „Antiproportionalität“ bedeutet. Das Wort „anti“ kommt aus dem griechischen und bedeutet so viel wie „gegen“. Und „Proportionalität“ beschreibt ein Verhältnis zwischen zwei Dingen. Dieses Verhältnis ist direkt, also beide Dinge/Größen steigen und fallen gleichmäßig.
Bei der Antiproportionalität haben wir ein „Gegenverhältnis“.
Die Antiproportionalität beschreibt ein (Gegen-)Verhältnis zwischen zwei Werten. Steigt einer der Werte, so fällt der andere. Fällt einer der Werte, so steigt der andere.
Man nennt die Antiproportionalität deswegen auch indirekte Proportionalität.
Schauen wir uns einige Beispiele hierzu an.
Beispiel: Ziegelstein-Transport
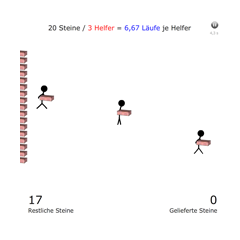
Eine Person soll 10 Ziegelsteine von einem Ort zu einem anderem Ort transportieren. Die Person kann immer nur 1 Ziegelstein gleichzeitig tragen. Wie oft muss die Person nun vom einem zum anderem Ort laufen?
Diese Frage lässt sich schnell beantworten: Die Person muss 10 mal laufen.
Was passiert aber, wenn die Person Hilfe bekommt und statt einer Person gleich 2 Personen die selbe Anzahl an Ziegelsteinen transportieren müssen? Was passiert, wenn 5 oder mehr Personen die Ziegelsteine transportieren? Wie oft muss jede einzelne Person dann laufen?
Die Antworten auf diese Fragen können wir uns wie folgt klar machen:
-
Für 10 Ziegelsteine läuft eine Person 10 mal. Rechnerisch:
10 Ziegelsteine : 1 Person ≙ 10 Läufe pro Person -
Für 10 Ziegelsteine laufen 2 Personen jeweils 5 mal. Rechnerisch:
10 Ziegelsteine : 2 Personen ≙ 5 Läufe pro Person -
Für 10 Ziegelsteine laufen 5 Personen jeweils 2 mal. Rechnerisch:
10 Ziegelsteine : 5 Personen ≙ 2 Läufe pro Person
Hier fällt uns etwas beim Verhältnis „Anzahl der Personen zu Anzahl der Läufe pro Person“ auf: Wenn sich die Anzahl der Personen erhöht, sinkt die Anzahl der Läufe pro Person.
Genau dieses „Gegenverhältnis“ ist es, was die Antiproportionalität ausmacht. Wenn wir genauer hinschauen, dann sehen wir auch, dass es einen Proportionalitätsfaktor gibt. Multiplizieren wir jeweils Anzahl Personen mit Anzahl an Läufen (siehe Beispiel oben) so erhalten wir:
1 · 10 = 10
2 · 5 = 10
5 · 2 = 10
Das Verhältnis verändert sich gleichmäßig. Verdoppeln wir die Anzahl der Personen, so brauchen wir nur die Hälfte der Läufe. Verfünffachen wir die Anzahl der Leute, so brauchen wir nur ein Fünftel der Läufe. Den Wert 10 nennt man in diesem Fall „Antiproportionalitätsfaktor“. Wir können eine beliebige Anzahl an Personen nehmen und diese mit der dazugehörigen Anzahl an Läufen multiplizieren und wir erhalten immer den selben Antiproportionalitätsfaktor.
Der Antiproportionalitätsfaktor des Verhältnisses ändert sich nicht. Er ist im Beispiel immer 10 Ziegelsteine.
Halten wir also fest:
Wenn Antiproportionalität bei einem Verhältnis vorliegt, dann gilt: Multiplizieren wir die eine Größe mit einem Wert, so müssen wir die andere Größe durch diesen Wert teilen.
Machen wir uns das noch an einem weiteren Beispiel klar.
Beispiel: Hausbau
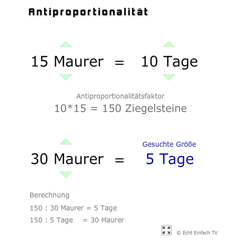
Unsere Aufgabe lautet: 20 Arbeiter bauen 10 Tage, um ein Haus fertigzustellen. Wie viele Tage benötigen 10 Arbeiter?
Diese Aufgabe können wir über den Antiproportionalitätsfaktor lösen.
20 Arbeiter ≙ 10 Tage
⇒ Antiproportionalitätsfaktor: 20 · 10 = 200
10 Arbeiter ≙ ? Tage
⇒ Antiproportionalitätsfaktor: 10 · ? = 200
Wir müssen also nur schauen, bei wie vielen Tagen wir den selben Antiproportionalitätsfaktor erhalten. Dafür brauchen wir nur eine Gleichung auflösen:
10 · x = 200
Stellen wir die Gleichung nach x um, so erhalten wir:
x = 200 : 10
x = 20
10 Arbeiter brauchen also 20 Tage.
Außerdem können wir die Aussage noch über den Dreisatz lösen. Wir berechnen dafür erst einmal, wie lange 1 Arbeiter braucht und anschließend, wie lange 10 Arbeiter brauchen:
20 Arbeiter brauchen 10 Tage.
1 Arbeiter braucht 20 mal so lange, also 10 · 20 Tage = 200 Tage
10 Arbeiter sind 10 mal so schnell, also 200 : 10 Tage = 20 Tage
Auch hier erhalten wir das selbe Ergebnis.
Antiproportionalität und Fläche
Wir können uns die Antiproportionalität auch anhand einer Fläche anschaulich machen. Wir haben ein Rechteck mit einem Flächeninhalt, der dem Antiproportionalitätsfaktor entspricht. Die beiden Seitenlängen entsprechen den beiden Größen unseres Verhältnisses. Jetzt ändern wir die beiden Seitenlängen des Rechtecks so, dass sich der Flächeninhalt sich nicht ändert - und damit auch nicht der Antiproportionalitätsfaktor. Wir vergrößern also die eine Seitenlänge um einen bestimmen Faktor und verringern dementsprechend die zweite Seitenlänge um den selben Faktor.
Anschaulich ist der Antiproportionalitätsfaktor als Fläche in dem folgende Programm dargestellt.
Zusammenfassung
Direkte Proportionalität
Zwei Mengen sind zueinander direkt-proportional, wenn sie zusammen gleichmäßig steigen oder fallen. Mit „gleichmäßig“ ist ein gleiches Verhältnis gemeint, also der Proportionalitätsfaktor, den wir ausrechnen können, indem wir beide Mengen miteinander dividieren. Dieser Wert muss stets konstant sein.
Indirekte Proportionalität
Zwei Menge sind zueinander indirekt-proportional, wenn die eine Menge steigt und die andere Menge im gleichen Maße fällt. Mit „gleichem Maße“ ist der Antiproportionalitätsfaktor gemeint, den wir ausrechnen können, indem wir beide Mengen miteinander multiplizieren. Dieser Wert muss stets konstant sein.
Beispiele für Antiproportionalität
Im Folgenden einige Beispiele für die Antiproportionalität:
- Um so mehr Zeit du Sport treibst, desto weniger wirst du wiegen.
- Um so mehr wir uns von einem Epizentrum (dem Startpunkt eines Erdbebens) entfernen, desto weniger Erschütterungen bemerken wir.
- Je weiter sich eine Welle auf dem Meer bewegt, desto kleiner wird sie.
- Um so mehr du dich wäschst, desto weniger Bakterien befinden sich auf deiner Haut.
Bei der direkten Proportionalität schreiben wir zwei Mengen a und b, die direkt voneinander abhängen, allgemein mit: a ~ b
Bei der Antiproportionalität schreiben wir die zwei Mengen, die indirekt proportional voneinander abhängen, allgemein mit: a ~ 1/b