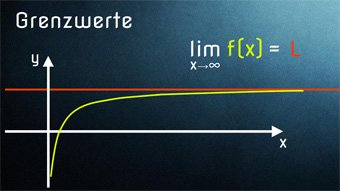
Nehmen wir uns das folgende Beispiel:
\( \lim \limits_{x\to 2} \frac{1}{x-2} = ? \)
Grafisch betrachtet:
.png)
Wir sehen hier, dass wir zwei unterschiedliche Grenzwerte haben, je nachdem von welcher Seite man sich den Grenzwert anschaut. Wenn wir von links kommen, haben wir den „linksseitigen Grenzwert“ mit -unendlich und wenn wir von rechts kommen, haben wir den „rechtsseitigen Grenzwert“ von +unendlich.
Auf den rechtsseitigen und linksseitigen Grenzwert wollen wir jetzt genauer eingehen.
Haben wir eine reelle Nullstelle zu untersuchen, so muss man sich stets beide Seiten einer zur untersuchenden Stelle anschauen, um sicherzustellen, dass ein beidseitiger Grenzwert vorliegt. Ein solcher liegt vor, wenn linksseitiger und rechtsseitiger Grenzwert übereinstimmen. Um den linksseitigen Grenzwert von dem rechtsseitigen zu unterscheiden, wird meist die Notation verwendet, dass man an den Stellenwert den man untersucht ein + (rechtsseitig) oder ein - (linksseitig) hochgestellt anfügt.
Wir untersuchen nun die Funktion \(f(x) = \frac{1}{x^2}\) an der Stelle x = 0.
\( \lim \limits_{x\to0^{+}} \frac{1}{x^2} = ? \)
\( \lim \limits_{x\to0^{-}} \frac{1}{x^2} = ? \)
Bestimmen wir dies mittels einer Wertetabelle:
Von rechts kommend:
| x | 1 | 0,5 | 0,1 | 0,01 |
| y | 1 | 4 | 100 | 10 000 |
Von links kommend:
| x | -1 | -0,5 | -0,1 | -0,01 |
| y | 1 | 4 | 100 | 10 000 |
Wir können nun die jeweiligen Grenzwerte bestimmen zu:
\( \lim \limits_{x\to0^{+}} \frac{1}{x^2} = +\infty \)
\( \lim \limits_{x\to0^{-}} \frac{1}{x^2} = +\infty \)
Da der rechtsseitige und der linksseitige Grenzwert übereinstimmen, dürfen wir also den beidseitigen Grenzwert ausdrücken mit:
\( \lim \limits_{x\to0} \frac{1}{x^2} = \infty \)