Unter einem Grenzwert einer Funktion f an einer Stelle x0 versteht man den Wert, dem sich die Funktion in der Umgebung dieses Punktes annähert.
Das heißt, man setzt nacheinander x-Werte in die Funktionsgleichung ein, die sehr nah an der zu untersuchenden Stelle liegen und schaut, wie sich die y-Werte (Funktionswerte) verhalten.
Oft macht man das an sogenannten Definitionslücken, bei denen die Funktion formal nicht definiert ist (zum Beispiel f(x) = \( \frac{1}{x} \) für x=0) oder man betrachtet das Verhalten der Funktion im Unendlichen, das heißt man überprüft, was mit dem Funktionswert passiert, wenn man nach und nach immer größere Zahlen für x einsetzt (bzw. immer kleinere, das ist dann der Grenzwert gegen minus unendlich.)
Man unterscheidet dabei zwischen sogenannten „eigentlichen Grenzwerten“, das sind Grenzwerte, die tatsächlich einer Zahl entsprechen, und „uneigentlichen Grenzwerten“, das heißt der Wert der Funktion geht gegen ±unendlich.
Der Begriff Grenzwert taucht in mehreren Gebieten der Mathematik auf, besonders jedoch bei den Funktionen. Im Folgenden mehr dazu.
Befasst man sich mit einer Kurvendiskussion (das ist eine ausführliche Untersuchung der Eigenschaften einer Funktion), so wird versucht, möglichst viele Informationen über die Funktionen zu gewinnen. Es stellt sich beispielsweise die Frage nach den Achsenschnittpunkten oder nach dem Monotonieverhalten.
Genauso kann die Frage auftreten, wie sich der Graph im Unendlichen verhält, um einen Überblick über den Graphen insgesamt zu erhalten. Dies kann man sich in erster Linie graphisch veranschaulichen. Betrachten wir uns dazu ein Beispiel:
(x+1).png)
(x+1)-zoom.png)
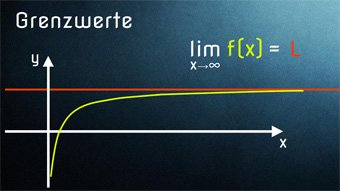
Wollen wir hier eine Aussage treffen, was passiert, wenn x sehr große Werte annimmt, so erkennen wir, dass sich der Graph mehr und mehr der Geraden y = 1 annähert.
Es fällt auf, dass der Graph dem Graphen y = 1 nur nahe kommt, ihn aber nie berührt oder schneidet.
Hier benötigen wir die Begriffe „Asymptote“ und „Grenzwert“.
Man betrachtet y = 1 als „Asymptote“ (die rote Gerade oben), da sich der Graphen nur an diese annähert, aber sie nie berührt oder schneidet. Wir merken uns:
Eine Asymptote ist eine Funktion, an die sich eine andere Funktion im Unendlichen annähert.
Der Wert 1 wird als Grenzwert beschrieben und gibt dem Betrachter, der den Graphen nicht sieht, einen Hinweis auf den Verlauf der Funktion.
Der Begriff Grenzwert kommt aus dem lateinischen „limes“ = Grenze, daher wird in der Mathematik die Kurzform lim benutzt, um anzuzeigen, dass man mit einem Grenzwert arbeitet.
Grenzwerte lassen sich rechnerisch bestimmen. Schauen wir uns das als nächstes an: Grenzwerte rechnerisch bestimmen