Bei der Primfaktorzerlegung wird eine natürliche Zahl als Multiplikation von Primzahlen geschrieben.
Beispiele:
- 10 = 2 · 5
- 20 = 2 · 2 · 5
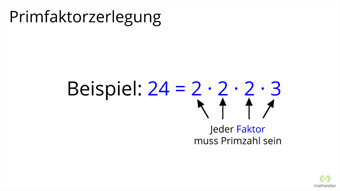
- 24 = 2 · 2 · 2 · 3
Faktoren der Multiplikation sind hier Primzahlen. Wir nennen sie „Primfaktoren“. Sie ergeben als Produkt die natürliche Zahl (auch „zusammengesetzte Zahl“).
Beispiele für Primfaktorzerlegungen
Nehmen wir uns einige Zahlen und zerlegen diese in ihre Primfaktoren:
1 = 1
2 = 2 ← Primzahl
3 = 3 ← Primzahl
4 = 2 · 2
5 = 5 ← Primzahl
6 = 2 · 3
7 = 7 ← Primzahl
8 = 2 · 2 · 2
9 = 3 · 3
10 = 2 · 5
11 = 11 ← Primzahl
12 = 2 · 2 · 3
…
100 = 2 · 2 · 5 · 5
1000 = 2 · 2 · 2 · 5 · 5 · 5
2000 = 2 · 2 · 2 · 2 · 5 · 5 · 5
78 977 = 78 977 ← Primzahl
78 978 = 2 · 3 · 13 163
Doch wie können wir die Primfaktoren von einer großen Zahl ermitteln? Schauen wir uns das im Folgenden an.
Primfaktorzerlegung von großen Zahlen
Wählen wir uns eine größere Zahl, zum Beispiel 1 300. Wie können wir die Primfaktoren ermitteln?
Dazu prüfen wir die Zahl auf Teilbarkeiten.
Zuerst fällt auf, dass die letzte Ziffer eine 0 ist, das heißt, 1 300 ist eine gerade Zahl und durch 2 teilbar.
1300 : 2 = 650
Wir können die 1 300 nun auch so schreiben:
1300 = 2 · 650
Jetzt betrachten wir die 650. Hier sehen wir auch, dass die letzte Ziffer eine 0 und die Zahl somit durch 2 teilbar ist. Tun wir dies:
650 : 2 = 325
Wir können die 1 300 nun auch so schreiben:
1300 = 2 · 650
1300 = 2 · 2·325
Nun untersuchen wir die 325. Hier erkennen wir, dass die letzte Ziffer eine 5 ist, somit ist die Zahl durch 5 teilbar. Dividieren wir entsprechend:
325 : 5 = 65
Wir können die 1 300 nun auch so schreiben:
1300 = 2 · 650
1300 = 2 · 2 · 325
1300 = 2 · 2 · 5·65
Jetzt geht es weiter mit der 65. Diese hat als letzte Ziffer auch eine 5, damit ist die Zahl durch 5 teilbar:
65 : 5 = 13
Wir können die 1 300 nun auch so schreiben:
1300 = 2 · 650
1300 = 2 · 2 · 325
1300 = 2 · 2 · 5 · 65
1300 = 2 · 2 · 5 · 5·13
Die 13 ist eine Primzahl. Hier lässt sich nichts weiter zerlegen.
Blicken wir auf alle Faktoren: 2 · 2 · 5 · 5 · 13, so erkennen wir, dass es sich bei allen Zahlen um Primzahlen handelt.
Die Primfaktorzerlegung haben wir also erfolgreich durchgeführt. Das Ergebnis:
1300 = 2 · 2 · 5 · 5 · 13
Wer prüfen möchte, ob eine Zahl tatsächlich Primzahl ist, der verwendet die Primfaktorzerlegung. Jede Zahl, die nicht zerlegt werden kann, ist eine Primzahl. Es gibt hierzu einen Primzahltester (Zahlenanalyse). Einfach eine Zahl eingeben und die Primfaktorzerlegung wird angezeigt, auch für sehr große Zahlen.
Hinweise
Primzahlen werden übrigens oft bei Verschlüsselungsverfahren angewendet (Codes der Kryptographie). In der Mathematik trifft man sie jedoch am häufigsten bei ggT und kgV an.
Achtung: Einige Schüler machen den Fehler und reden von „Primzahlzerlegung“, was jedoch falsch ist. Denn eine Primzahl lässt sich nicht in weitere Primzahlen zerlegen, da sie nur durch sich selbst und durch 1 teilbar ist.