Primzahlen

Schauen wir uns die Teilbarkeit der 7 an:

7 : 1 = 7 ✓
7 : 2 = 3 Rest 1 ⛔
7 : 3 = 2 Rest 1 ⛔
7 : 4 = 1 Rest 3 ⛔
7 : 5 = 1 Rest 2 ⛔
7 : 6 = 1 Rest 1 ⛔
7 : 7 = 1 ✓

Die einzigen Teiler der 7 sind also 1 und 7.

Im Gegensatz dazu die Zahl 6:

6 : 1 = 6 ✓
6 : 3 = 2 ✓
6 : 2 = 3 ✓
6 : 4 = 1 Rest 2 ⛔
6 : 5 = 1 Rest 1 ⛔
6 : 6 = 1 ✓

Die Teiler der 6 sind also 1, 2, 3 und 6. Sie ist damit keine Primzahl, sondern eine zusammengesetzte Zahl (und zwar 6 = 2 · 3).

Schlussfolgerung:

Es gibt Zahlen, die in Multiplikationen zerlegbar sind, man nennt sie „zusammengesetzte Zahlen“. Zum Beispiel: 4 = 2 · 2

Und es gibt Zahlen, die sich nicht in Multiplikationen zerlegen lassen, man nennt sie „Primzahlen“. Zum Beispiel: 7 = 7

Weitere Primzahlen sind 2, 3, 5, 7, 11, 13, …

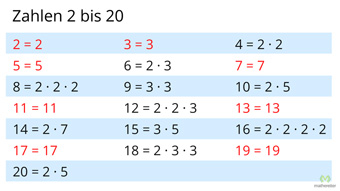
Schauen wir uns die natürlichen Zahlen an und zerlegen diese so weit wie möglich in Faktoren von anderen Zahlen.

• 2 nicht zerlegbar
• 3 nicht zerlegbar
• 4 zerlegbar in 2 · 2
• 5 nicht zerlegbar
• 6 zerlegbar in 2 · 3
• 7 nicht zerlegbar
• 8 zerlegbar in 2 · 2 · 2
• 9 zerlegbar in 3 · 3
• 10 zerlegbar in 2 · 5
• 11 nicht zerlegbar
• 12 zerlegbar in 2 · 2 · 3
• 13 nicht zerlegbar
• 14 zerlegbar in 2 · 7
• 15 zerlegbar in 3 · 5
• 16 zerlegbar in 2 · 2 · 2 · 2
• 17 nicht zerlegbar
• 18 zerlegbar in 2 · 3 · 3
• 19 nicht zerlegbar
• 20 zerlegbar in 2 · 2 · 5
• 21 zerlegbar in 3 · 7

Die Zahl 1 fehlt in obiger Aufstellung, denn die 1 ist keine Primzahl.

Es gibt bis zur Zahl 100 insgesamt 25 Primzahlen, also Zahlen, die nicht in Multiplikationen zerlegbar sind. Nachstehend sind sie aufgelistet:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

Die Zahl 2 ist übrigens die einzige gerade Primzahl.

Alle anderen Primzahlen sind ungerade.

Wenn wir uns die Teiler der Primzahlen anschauen, erkennen wir, dass die Primzahlen nur durch 1 und durch sich selbst teilbar sind. Und genau das ist der Merksatz für die Primzahlen:

Beispiele von Primzahlen

• 7 = 7 · 1
• 19 = 19 · 1
• 31 = 31 · 1
• 109 = 109 · 1

Beispiele von zusammengesetzten Zahlen

Hat eine natürliche Zahl neben sich selbst und der 1 weitere Teiler, so ist sie eine zusammengesetzte Zahl und keine Primzahl.

• 30 = 2·3·5
• 44 = 2·2·11
• 60 = 2·2·3·5
• 82 = 2·41

Wortherkunft Primzahl

Das Wort „prim“ kommt vom lateinischen „prima“, das wiederum von „primus“ stammt und „Erster, Vorderster“ bedeutet. Wahrscheinlich wurde diese Bezeichnung gewählt, da jede natürliche Zahl aus Primzahlen besteht, sie sind sozusagen die Atome der Zahlenwelt.