Wie wir bereits bei der Einführung zu den Primzahlen erfahren haben, gibt es Zahlen, die man in Multiplikationen zerlegen kann, sie heißen „zusammengesetzte Zahlen“, und es gibt Zahlen, die sich nicht in Multiplikationen zerlegen lassen, man nennt sie „Primzahlen“.
Um Primzahlen zu ermitteln, gibt es verschiedene Methoden.
Im Folgenden sei die Methode namens „Sieb des Eratosthenes“ vorgestellt.
Sieb des Eratosthenes
Eine der ersten Methoden hatte der Mathematiker Eratosthenes bekannt gemacht, diese Methode heißt daher „Sieb des Eratosthenes“.
Bei diesem Verfahren werden alle Vielfachen (beginnend bei der Zahl 2) weggestrichen, da Vielfache keine Primzahlen sein können, denn sie haben mehr als zwei Teiler (also nicht nur 1 und sich selbst, so wie bei den Primzahlen gefordert).
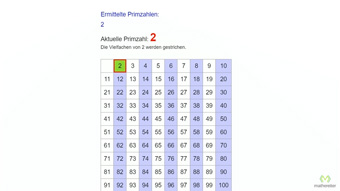
Nachfolgendes animiertes Programm zeigt das Verfahren vom „Sieb des Eratosthenes“:
Programm starten
Ermittelte Primzahlen: …
Aktuelle Primzahl:
Die Vielfachen von werden gestrichen.
Wir beginnen mit den Vielfachen von 2 (also 2, 4, 6, 8, …).
Danach folgen die Vielfachen der Zahl 3 (also 3, 6, 9, … die 6 wurde bereits gestrichen, da 6 auch ein Vielfaches der Zahl 2 ist).
Alle Zahlen, die nicht weggestrichen worden sind, sind Primzahlen.
Alle Zahlen, die weggestrichen worden sind, sind Vielfache von Primzahlen.
Genau so verfährt das Programm oben: Sofern eine Zahl als Vielfaches weggestrichen ist, wird sie nicht mehr betrachtet.