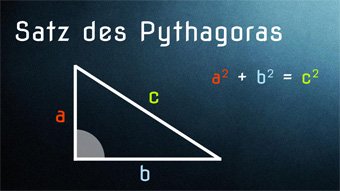
Der Satz des Pythagoras lässt sich auf viele Weisen grafisch herleiten. Nachstehend ein Beweis ausführlich festgehalten. Diese Grafik hilft zum Verstehen:

Zeichnet man ein großes Quadrat, bei dem jede der Seiten aus den Teilstrecken a und b besteht, erhält man für die Quadratsfläche die Formel (a+b)·(a+b). Diese Flächenformel lässt sich mittels der 1. Binomischen Formel ausmultiplizieren zu: (a+b)·(a+b) = a² + 2·a·b + b²
Gleichfalls ergibt sich die gesamte Quadratsfläche (a+b)·(a+b) aber auch, wenn wir die weiße Quadratsfläche c² und die 4 Dreiecksflächen addieren. Dies kann als Gleichung wie folgt festgehalten werden: c² + 4 · (a·b : 2). Daraus erhalten wir: c² + 2·a·b
Beide vorgenannten Flächen entstammen aus (a+b)·(a+b), sind also gleich groß. Wir dürfen sie demnach gleichsetzen:
(a+b)·(a+b) = (a+b)·(a+b)
a² + 2·a·b + b² = c² + 2·a·b
Wenn wir nun auf beiden Seiten der Gleichung 2·a·b abziehen, erhalten wir:
a² + b² = c² → der Satz des Pythagoras.
Hier sei noch ein Zahlenbeispiel zum Beweis gegeben:

Nachweis für Quadratsfläche c²
Wenn wir die vier grünen rechtwinkligen Dreiecke in das große Quadrat (a+b)² legen, warum ergibt sich dann eigentlich ein Quadrat im Inneren (mit den Seiten c)?
Diese Frage können wir beantworten, indem wir den Winkelsummensatz nutzen. Der Winkelsummensatz besagt, alle Innenwinkel eines Dreiecks müssen zusammen 180° ergeben. Ist ein Winkel rechtwinklig, müssen die beiden nicht-rechtwinkligen Winkel (Alpha und Beta) zusammen 90° sein.
Bei der folgenden Grafik können wir erkennen, dass Alpha und Beta unten auf der Seite des großen Quadrats liegen und mit dem orangen Winkel einen gestreckten Winkel von 180 Grad bilden. Da α + β + oranger Winkel = 180° sein müssen, kann der orange Winkel als Teil des gestreckten Winkels nur eine Größe von 90° (also γ) haben: