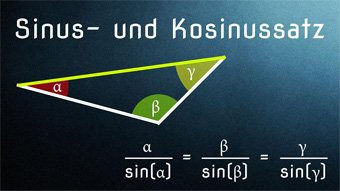
Wir hatten bei Sinus und Kosinus gelernt, dass der Sinus/Kosinus nur für rechtwinklige Dreiecke definiert ist. Jetzt fragt sich, ob wir Sinus und Kosinus auch bei allgemeinen Dreiecken verwenden können.
Zur Erinnerung: Ein allgemeines Dreieck ist ein beliebiges Dreieck, bei dem die Winkel beliebige Werte annehmen können. Zum Beispiel:
Beim Betrachten von allgemeinen Dreiecken fällt auf, dass wir jedes allgemeine Dreieck durch das Einzeichnen einer Höhe in zwei rechtwinklige Dreiecke aufteilen können:
Damit lässt sich jedes allgemeine Dreieck über die beiden rechtwinkligen Teildreiecke berechnen, also dessen Seiten, Winkel und Flächen. Wir können uns diese Arbeit aber abkürzen.