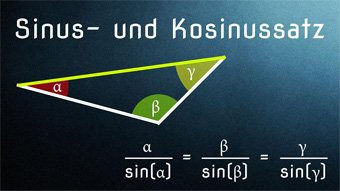
Den Sinussatz hatten wir bereits hergeleitet, er lautet:
$$ \frac{a}{sin(α)} = \frac{b}{sin(β)} = \frac{c}{sin(γ)} $$
Man kann ihn formulieren als:
Die Dreiecksseiten verhalten sich zueinander wie die Sinuswerte ihrer Gegenwinkel.
Die Herleitung in einer Grafik zusammengefasst:

An dieser Stelle kann man gleichsetzen und erhält:
h = h
sin(γ) · a = sin(α) · c
Dann noch umstellen und wir erhalten den Sinussatz für a und c:
sin(γ) · a = sin(α) · c | :a und :c
sin(γ) : c = sin(α) : a | :a und :c
Noch als Bruch notiert:
sin(γ) / c = sin(α) / a
Entsprechend leitet man sich das Verhältnis für b und Winkel β her.