Beim Aufstellen von linearen Funktionen ist es von großer Bedeutung, dass man in der Lage ist, die notwendigen Informationen aus dem Text herauszuziehen. Dabei können wichtige Hinweise in Begriffen wie „parallel“ oder „senkrecht“ versteckt sein.
Aufgabe: Parallele Geraden
So mag eine Aufgabe beispielsweise lauten:
„Bestimme die lineare Funktion durch den Punkt A(2|3), welche parallel zur Geraden g(x) = 2·x + 3 ist.“
Uns muss nun bewusst sein, dass „parallel“ ein anderes Wort für „haben die gleiche Steigung“ ist. Somit ist aus der Aufgabe die Information herauszulesen: „Die gesuchte Gerade geht durch den Punkt A(2|3) und sie hat die Steigung m = 2.“
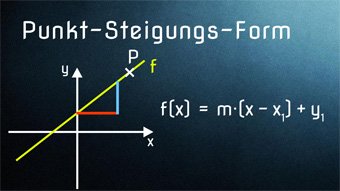
Mit einem der Lösungsverfahren (Punktsteigungsform bietet sich hier an) erhält man die gesuchte Gerade: f(x) = 2·x - 1

Aufgabe: Senkrechte Geraden
Um ein Beispiel mit „senkrecht“ anzuführen, könnte eine Aufgabe lauten:
„Die gesuchte Gerade geht durch den Punkt A(2|3) und steht senkrecht auf g(x) = 2·x + 3.“
Die Steigung der gesuchten Geraden lässt sich fast direkt ablesen. Dazu muss man sich erinnern, dass für zwei senkrecht aufeinander stehende Geraden gilt: m1 · m2 = -1 (vgl. Schnittpunkte von linearen Graphen).
Wir kennen nun m1 = 2, somit ist m2 = -1/2.
Mit der nun vorhandenen Steigung können wir uns der Punktsteigungsform bedienen und die gesuchte Gerade zu f(x) = -1/2·x + 4 bestimmen.