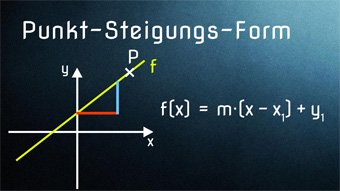
Haben wir nun nicht die Steigung gegeben, sondern stattdessen zwei Punkte, so können wir ebenfalls die Gleichung der linearen Funktion aufstellen.
Hierzu ist jedoch eine andere Formel zu verwenden, und zwar die Zweipunkteform. Diese lautet:
\( f(x) = \frac{ y_2 - y_1 }{ x_2 - x_1 } · (x - x_1) + y_1 \)
Dabei ist der erste Faktor \( \frac{ y_2 - y_1 }{ x_2 - x_1 } \) nichts anderes als die Steigung m, wie wir sie bereits kennengelernt haben.
Die Anwendung der Formel sieht an einem Beispiel dann so aus:
„Bestimme die lineare Funktion, die durch die Punkte A(1|2) und B(4|5) geht“.
\( f(x) = \frac{ y_2 - y_1 }{ x_2 - x_1 } · (x - x_1) + y_1 \)
\( f(x) = \frac{ 5 - 2 }{ 4 - 1 } · (x - 1) +2 \\ f(x) = \frac{3}{3} · (x - 1) + 2 \\ f(x) = 1 · (x - 1) + 2 \\ f(x) = x - 1 + 2 \\ f(x) = x + 1 \)
Die Gleichung dieser linearen Funktion lautet also:
f(x) = x + 1