Koordinatensysteme spielen eine wichtige Rolle in der Mathematik, aber auch in allen anderen Wissenschaften. Möchten wir Graphen, Diagramme, Pfeile (Vektoren) usw. zeichnen, benötigen wir ein Koordinatensystem.
Koordinatensysteme eignen sich hervorragend, um Zusammenhänge darzustellen, Daten auszuwerten und Geometrie zu visualisieren.
Wir betrachten uns hier das Koordinatensystem in einer Ebene.
Das Koordinatensystem wird zu Ehren von Réné Descartes „kartesisches Koordinatensystem“ genannt (also von Descartes kommt Kartesisch).
Descartes ist übrigens auch bekannt für die philosophische Erkenntnis „cogito ergo sum“ („Ich denke, also bin ich.“).
Alternativ kann man das kartesische Koordinatensystem auch „rechtwinkliges Koordinatensystem“ nennen.
Das Koordinatensystem im Raum (also in 3D) schauen wir uns im Artikel Punkte im Raum an.
Aufbau des Koordinatensystems
Ein kartesisches Koordinatensystem wird meist so gezeichnet:

Das kartesische Koordinatensystem ist wie folgt aufgebaut:
- eine Achse von links nach rechts (sie heißt „x-Achse“ oder auch „Abszisse“)
- eine Achse von unten nach oben (sie heißt „y-Achse“ oder auch „Ordinate“)
- die Koordinatenlinien sind horizontale und senkrechte Geraden, die in gleichen Abständen angeordnet sind
- x- und y-Achse haben Beschriftungen für die Abstände (meist 1, 2, 3, …)
- x- und y-Achse haben einen Pfeil am Ende
- die Abstände auf einer Achse müssen alle gleich groß sein (Abstand und Einheit kann man selbst festlegen, z. B. 1 als 1 cm)
- eine Position wird mit (x|y) angegeben, man nennt diese Angabe „x- und y-Koordinaten“
- durch die Achsen entstehen 4 Bereiche, die wir „Quadranten“ nennen
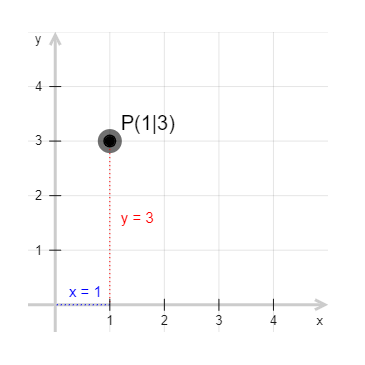
Durch die Einteilungen der x-Achse und y-Achse kann jedem Punkt eine x-Koordinate und eine y-Koordinate zugewiesen werden. Auf diese Weise lassen sich beliebige Positionen bestimmen.
Bewege den Punkt namens P und achte darauf, wie sich seine x- und y-Koordinaten verändern:
Der Punkt, wo sich x-Achse und y-Achse schneiden, heißt „Koordinatenursprung“. Er liegt bei (0|0).
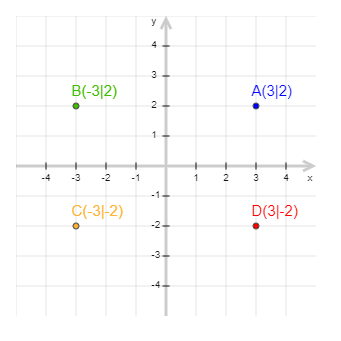
Nachfolgend sehen wir ein vollständig gezeichnetes Koordinatensytem mit 4 Quadranten:
Bewege die Punkte A, B, C und D und achte darauf, wie sich ihre positiven und negativen Koordinaten verändern: