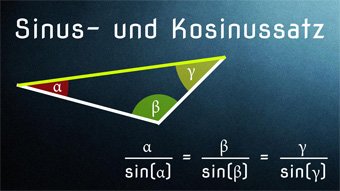
Der Sinussatz reicht nicht immer aus, um ein Dreieck berechnen zu können.
Für \( \frac{a}{\sin(α)} = \frac{b}{\sin(β)} \) haben wir zwei Varianten:
Variante A:
Wir brauchen entweder 1 Seite (a) und 2 Winkel (α und β), um die andere Seite (b) zu bestimmen.
Variante B:
Wir brauchen 2 Seiten (a, b) und 1 Winkel (α), um den anderen Winkel (β) zu bestimmen.
Neue Variante:
Was ist jedoch, wenn wir nur die Seiten a und c sowie Winkel β gegeben haben?
Der Sinussatz sieht dann so aus (die gegebenen Werte sind blau gefärbt) und lässt sich nicht berechnen:
\( \frac{ \textcolor{blue}{a} }{ \sin(α) } = \frac{ b }{ \sin(\textcolor{blue}{β}) } = \frac{ \textcolor{blue}{c} }{ \sin(γ) } \)
Können wir eine Formel aufstellen, die nur a, c und den Winkel β enthält? Denn dann ließen sich die anderen Winkel bestimmen.
Die Antwort ist ja. Schauen wir uns an, wie sich diese Formel (der sogenannte Kosinussatz) ergibt.