Lesezeit: 7 min
Matheretter
Je nach den gegebenen Werten in der Aufgabe müssen wir entscheiden, ob wir den Sinussatz
oder den Kosinussatz anwenden.
Hierzu eine Tabelle zur Übersicht:
|
Gegeben
|
Direkt zu berechnen
|
Lösungsweg
|
|
3 Seiten (SSS)
|
1 Winkel
|
Kosinussatz
|
|
2 Seiten und eingeschlossener Winkel (SWS)
|
1 Seite
|
Kosinussatz
|
|
2 Seiten und gegenüberliegender Winkel (SSWg)
|
1 Winkel (gegenüber der kleineren Seite)
|
Sinussatz
|
|
1 Seite und 2 Winkel (SWW)
|
1 Seite
|
Sinussatz
|
|
3 Winkel (WWW)
|
nicht lösbar, unendlich viele Möglichkeiten
|
-
|
Die nächste Übersicht zeigt konkret auf, welche gegebenenen Werte wir haben und wie wir zu der fehlenden Seite bzw. Winkel gelangen:
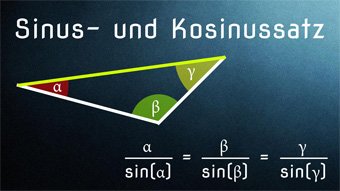
Alle Seiten und Winkel am Dreieck: a, b, c, α, β, γ
Fall 1: Gegeben 3 Seiten
Es sind drei Seiten des Dreiecks gegeben. Folgende Möglichkeiten der Berechnung:
Lösung mit: Kosinussatz
Fall 2: Gegeben 2 Seiten und eingeschlossener Winkel
Lösung mit: Kosinussatz
Fall 3: Gegeben 2 Seiten und 1 gegenüberliegender Winkel
Lösung mit: Sinussatz
Fall 4: Gegeben 2 Winkel und gegenüberliegende Seite
Lösung mit: Sinussatz
Fall 5: Gegeben 3 Winkel und keine Seite
Lösung: nicht lösbar, unendlich viele Möglichkeiten für a, b, c
Eindeutigkeit
Der Vorteil des Kosinussatzes ist, dass die Werte immer eindeutig sind.
Man erhält für die Winkelberechnung einen Wert von 0° bis 180°.
Beim Sinussatz hingegen erhält man stets einen Winkel von 0° bis 90° und muss das Ergebnis rechnerisch
bzw. mit der gegebenen Zeichnung überprüfen.
Sofern es sich um ein stumpfwinkliges Dreieck handelt, ist der Winkel ggf. per Identität umzuwandeln.
Also zum Beispiel statt 45°, dann 180° - 45° = 135° als Ergebnis.