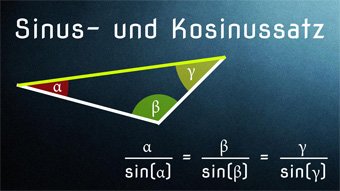
Es sei uns ein allgemeines Dreieck gegeben, in dem wir die Höhe hc einzeichnen. Gesucht sei der Zusammenhang zwischen a, b und c. Wir suchen einen Ausdruck für b2, der nur von a, b und den drei Winkeln α, β, γ abhängt.
Drücken wir zuerst Seite b über den Satz des Pythagoras aus:
b2 = h2 + d2
Drücken wir a über den Pythagoras aus:
a2 = h2 + e2
Nun stellen wir die Formel von a2 nach h2 um:
h2 = a2 - e2
Jetzt können wir dieses h2 in die Formel von b2 einsetzen:
b2 = h2 + d2 | h2 = a2 - e2
b2 = (a2 - e2) + d2
Das d stört noch, schauen wir auf das Dreieck, wir erkennen, dass sich d als Teilstrecke von c ergibt. Die Strecke d ergibt sich mit: d = c - e. Setzen wir diese für d ein:
b2 = (a2 - e2) + d2 | d = c - e
b2 = (a2 - e2) + (c - e)2
b2 = a2 - e2 + c2 - 2ce + e2
b2 = a2 - e2 + e2 + c2 - 2ce
b2 = a2 + c2 - 2ce
Als nächstes gilt es noch das e zu ersetzen. Erinnern wir uns, wir wollen eine Formel, die nur 3 Seiten und einen Winkel benötigt. e können wir über den Kosinus von β ausdrücken:
cos(β) = AK⁄HY = e⁄a
Dies nach e umgestellt: e = cos(β) · a
Setzen wir dies in unsere aktuelle Formel ein:
b2 = a2 + c2 - 2·c·e | e = cos(β) · a
b2 = a2 + c2 - 2·c·(cos(β) · a)
b2 = a2 + c2 - 2·a·c·cos(β)
Und dies ist auch schon der Kosinussatz. Wir haben alle 3 Seiten des Dreiecks (a, b, c) und nur 1 Winkel in der Formel. So lässt sich nun, wenn wir 2 Seiten gegeben haben und den einschließenden Winkel die 3. Seite berechnen. Oder wenn wir alle 3 Seiten gegeben haben, können wir einen fehlenden Winkel berechnen (und dann alle anderen).