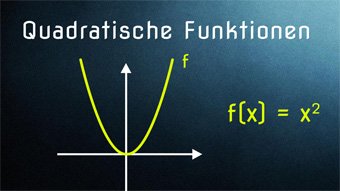
Wir können die Normalparabel nicht nur verschieben, wir können sie auch stauchen bzw. strecken. Hierzu multiplizieren wir einen Faktor zu dem x².
Die Gleichung sieht dann allgemein so aus: f(x) = a·x².
Bei der folgenden Grafik könnt ihr die Normalparabel stauchen und strecken. Einfach den schwarzen Punkt rechts verschieben. Achtet darauf, wie sich der Wert vor dem x² verändert:
Wenn der Wert vor x² größer als 1 ist, dann wird die Parabel gestreckt (also „dünner“).
Wenn der Wert vor x² exakt 1 ist, dann haben wir die unveränderte Normalparabel.
Ist der Wert vor x² zwischen 0 und 1 groß, so ist die Parabel gestaucht (also „breiter“).
Den Faktor vor dem x² nennen wir „Formfaktor“, da er für die Form (Stauchung und Streckung) der Parabel entscheidend ist.
Wertetabelle einer gestreckten Normalparabel
Die Wertetabelle zeigt die x-Werte von -4 bis +4. Wenn wir eine Streckung haben (nachfolgend mit 2·x²), so müssen wir diese wie folgt berücksichtigen:
| x | 2·x² | Punkt |
|---|---|---|
| -4 | 2·16 | P(-4|32) |
| -3 | 2·9 | P(-3|18) |
| -2 | 2·4 | P(-2|8) |
| -1 | 2·1 | P(-1|2) |
| 0 | 2·0 | P(0|0) |
| 1 | 2·1 | P(1|2) |
| 2 | 2·4 | P(2|8) |
| 3 | 2·9 | P(3|18) |
| 4 | 2·16 | P(4|32) |