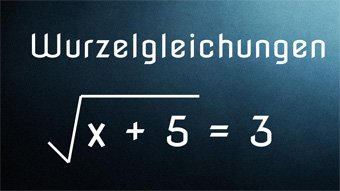Lösen wir eine Wurzelgleichung mit verschachtelter Wurzel:
\( \sqrt { -x+\sqrt { -x + 5 } } = 4 \)
Wir quadrieren beide Seiten und bringen das x auf die rechte Seite:
\( \sqrt { -x+\sqrt { -x + 5 } } = 4 \quad |{ () }^{ 2 } \\ -x+\sqrt { -x + 5 } = 16 \quad |+x \\ \sqrt { -x + 5 } = 16 + x \)
Wir können nun noch einmal quadrieren und auf der rechten Seite die binomische Formel anwenden:
\( \sqrt { -x + 5 } = 16 + x \quad | { () }^{ 2 } \\ -x + 5 = 256 + 32·x + { x }^{ 2 } \quad |+x -5 \\ { x }^{ 2 } + 33·x + 251 = 0 \)
Mit der p-q-Formel erhalten wir:
x1 ≈ -11,8902
x2 ≈ -21,1098
Durch die Probe stellen wir fest, dass nur x = -11,8902 die Gleichung löst.