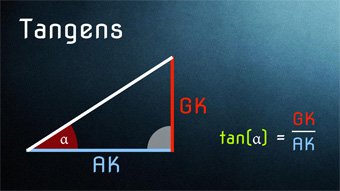
Gegeben sind a = 5 cm und b = 4,2 cm. Wir sollen den Winkel β bestimmen.
Wir nutzen sofort den Tangens hierfür:
tan(β) = GK⁄AK
tan(β) = b⁄a
tan(β) = 4,2 cm⁄5 cm
tan(β) = 0,84
Nun wissen wir, dass die Gegenkathete 0,84 mal so lang ist wie die Ankathete. Nutzen wir nun den Arkustangens, um den dazugehörigen Winkel zu bestimmen:
tan(β) = 0,84 | tan-1
tan-1(tan(β)) = tan-1(0,84)
β = tan-1(0,84)
β ≈ 40°
Der gesuchte Winkel β ist also rund 40° groß.
Hinweis: Wir müssen darauf achten, dass der Taschenrechner den Modus DEG (Gradmaß) anzeigt und nicht RAD (Radiant/Bogenmaß).