Stellen wir uns vor, wir haben ein rechtwinkliges Dreieck gegeben mit Längenangaben für Seite a und Seite b.
Um den Winkel β zu bestimmen, können wir jetzt nicht den Sinus benutzen, denn dieser verlangt die Angabe der Seiten b und c, also \( \sin(β) = \frac{b}{c} \).
Auch der Kosinus hilft uns nicht weiter, denn dieser benötigt die Seiten a und c, also \( \cos(β) = \frac{a}{c} \).
Um den Winkel β direkt aus den Seiten a und b berechnen zu können, verwenden wir den sogenannten Tangens:
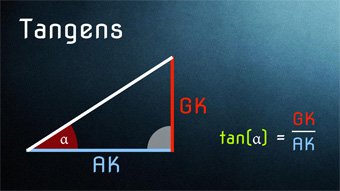
\( \tan(β) = \frac{\text{GK}}{\text{AK}} \)
\( \tan(β) = \frac{b}{a} \)
Tangens als Verhältnis Gegenkathete / Ankathete
Der Tangens ist das Verhältnis von Gegenkathete zu Ankathete.
Wie auch beim Sinus und Kosinus, ist der Tangenswert bei festem Winkel immer gleich, egal wie groß wir unser rechtwinkliges Dreieck wählen.
Ein Beispiel mit Winkel β = 30°:
Der Tangens lautet tan(30°) ≈ 0,577.
Dies besagt, dass die Gegenkathete 0,577 mal so lang ist wie die Ankathete.
Zeichnen wir ein Dreieck mit Beispielwerten hierzu:
HY = 11,54 cm
GK = 5,77 cm
AK = 10 cm
\( \tan(30°) = \frac{\text{GK}}{\text{AK}} = \frac{5,77 \text{ cm}}{10 \text{ cm}} = 0,577 \)
\( \frac{\text{GK}}{\text{AK}} = 0,577 \\ \text{GK} = 0,577 · \text{AK} \)
Selbst wenn wir jetzt andere Seitenlängen wählen, doch den Winkel bei 30° lassen, ändert sich das Verhältnis von Gegenkathete zu Ankathete nicht.
tan(30°) ist weiterhin 0,577. Also die Gegenkathete ist bei 30° immer 0,577 mal so lang wie die Ankathete.
Ein weiteres Beispieldreieck:
HY = 8,66 cm
GK = 4,33 cm
AK = 7,5 cm
\( tan(30°) = \frac{\text{GK}}{\text{AK}} = \frac{4,33 \text{ cm}}{7,5 \text{ cm}} ≈ 0,577 \)
\( \frac{ \text{GK} }{ \text{AK} } = 0,577 \\ \text{GK} = 0,577 · \text{AK} \)