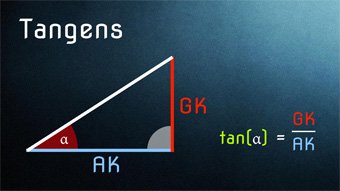
Wir wissen nun, dass der Tangens der Steigung entspricht. Jetzt können wir jederzeit den Steigungswinkel aus dem Steigungswert (dem Tangenswert) bestimmen.
Gegeben ist die Funktionsgleichung: f(x) = 1,6·x und gefragt ist nach dem Winkel, mit dem diese Funktion steigt.
Um den Steigungswinkel zu bestimmen, legen wir fest:
f(x) = 1,6·x
f(x) = m·x
f(x) = tan(β)·x
tan(β) = 1,6 | Arkustangens verwenden: tan-1()
tan-1(tan(β)) = tan-1(1,6)
β = tan-1(1,6)
β ≈ 58°
Der Graph der Funktion steigt also mit 58°. Er sieht wie folgt aus: