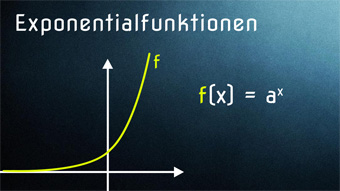
Es gibt drei Fälle von Verläufen für die Exponentialfunktion f(x) = ax zu einer positiven Basis a:
Fall 1 mit a = 1
Dann ist f(x) = 1x = 1. Wir erhalten also eine konstante Funktion.
~plot~ 1^x;hide ~plot~
Da sich eine konstante Funktion ergibt, schließt man die 1 per Definition aus, also: a ∈ R \ { 1 }
Fall 2 mit a > 1
Dann erhalten wir eine streng monoton wachsende Funktion. Die y-Werte sind alle positiv und reell. Beispiele: f(x) = 3x; g(x) = 5x
~plot~ 3^x;5^x;hide ~plot~
Hier kann man gut einen Wachstumsprozess erkennen.
Fall 3 mit 0 < a < 1
Dann erhalten wir eine streng monoton fallende Funktion. Die y-Werte sind alle positiv und reell. Beispiele: f(x) = (1/3)x; g(x) = (1/5)x
~plot~ (1/3)^x;(1/5)^x;hide ~plot~
Hier kann man gut einen Zerfallsprozess erkennen.