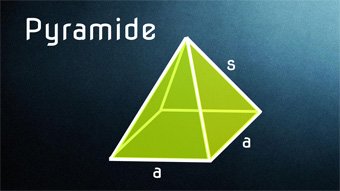
Die Diagonale d ist uns schon von den Quadraten her bekannt. Bei einer quadratischen Pyramide haben wir eine quadratische Grundfläche:

Wenn wir die Diagonale d mit Hilfe der Seite a ausdrücken wollen, so wenden wir den Satz des Pythagoras an:
d² = a² + a²
Dann lösen wir die Gleichung nach d auf:
\( d^2 = a^2 + a^2 \\ d = \sqrt{a^2 + a^2} \\d = \sqrt{2·a^2} \\ d = \sqrt{2} · \sqrt{a^2} \\ d = \sqrt{2} · a \)
Es ergibt sich damit die Diagonalenformel: d = √2·a.