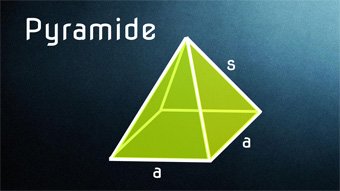
Die quadratische Pyramide besitzt 4 Seitenkanten (auch Mantellinien genannt).
Die Länge einer Seitenkante s kann über die Höhe h und die Seite a berechnet werden, wenn man sich den Satz des Pythagoras zur Hilfe nimmt.

Das Dreieck, das man hier erkennt, bildet sich aus der gesuchten Seite s, der Höhe h und der Strecke x.
Die Formel gemäß Satz des Pythagoras lautet demnach: s² = h² + x²
Das x stellt dabei die halbe Diagonale der Grundfläche dar. Wir wissen, dass sich die Diagonale berechnet mit \( d = \sqrt{2·a^2} = \sqrt{2}·a \). Damit ist die Hälfte der Diagonale: \( x = \frac{d}{2} = \frac{\sqrt{2}·a}{2} = \sqrt{2}·a : 2 = \sqrt{2} · \frac{a}{2} \).

Quadriert man jetzt x gemäß Pythagoras, so erhält man:
\( x^2 = ( \sqrt{2} · \frac{a}{2} )^2 = \sqrt{2}^2 · (\frac{a}{2})^2 = 2 · \frac{a^2}{4} = \frac{a^2}{2} \)
Setzen wir \( \textcolor{#00F}{x^2} = \textcolor{#00F}{ \frac{a^2}{2} } \) in die Formel s² = h² + x² ein, so ergibt sich:
\( \begin{aligned} s^2 &= h^2 + x^2 \qquad | \sqrt{ \ } \\ \sqrt{s^2} &= \sqrt{h^2 + x^2} \\ s &= \sqrt{h^2 + \textcolor{#00F}{x^2}} \\ s &= \sqrt{h^2 + \textcolor{#00F}{ \frac{a^2}{2} } } \end{aligned} \)