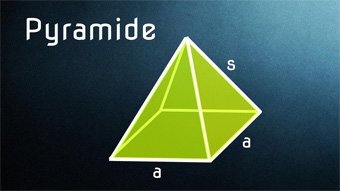
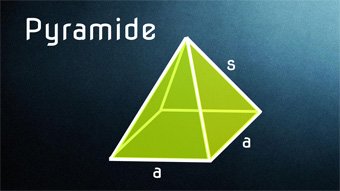
Um eine Pyramide beschreiben zu können, gibt es einige Begriffe, die man kennen muss. Das sind unter anderem die bekannten Begriffe wie „Mantelfläche“, „Oberfläche“ und „Volumen“, doch gibt es speziell bei den Pyramiden auch die Bezeichnungen “Seitenkante” oder auch „Höhe der Seitenfläche“. Eine Sammlung all dieser Begriffe und die zugehörigen Formeln seien im folgenden Schaubild aufgeführt.

Link zur Grafik: https://www.matheretter.de/img/wiki/pyramide-formeln.png
Die von uns betrachtete “gerade quadratische Pyramide” besteht also aus einer quadratischen Grundfläche mit der Grundseite a. Das “gerade Pyramide” liefert zudem den Hinweis, dass die Spitze sich genau über dem Mittelpunkt der Grundfläche befindet, was durch die Höhe h beschrieben wird. Schauen wir uns im Folgenden die Formeln genauer an, wobei wir davon ausgehen, dass a und h immer gegeben seien.
Umfang u
Der Umfang entspricht ebenfalls dem eines Quadrats und ist mit u = 4·a anzugeben.
Diagonale d
Die Diagonale d ist uns schon von den Quadraten her bekannt. Wir haben hier eine quadratische Grundfläche und es ergibt sich damit d = √2·a.

Höhe ha
Die Pyramide besitzt nicht nur eine Höhe im Allgemeinen, sondern auch die Seitenflächen haben eine Höhe. Diese Dreieckshöhen ha kann man mit Hilfe von a und h berechnen, wenn man nach rechtwinkligen Dreiecken Ausschau hält, um damit dann schließlich den Satz des Pythagoras anwenden zu können.

Mit dem Satz des Pythagoras ergibt sich daraus:
\( h_a = \sqrt{h^2 + \frac{a}{2}^2} \)
Seitenkante/Mantellinie s
Die quadratische Pyramide besitzt 4 Seitenkanten (auch Mantellinien genannt). Auch hier kann die Länge über h und a ausgedrückt werden, wenn man sich wiederum den Satz des Pythagoras zur Hilfe nimmt.

Das Dreieck, das man hier erkennen sollte, bildet sich aus der gesuchten Seite s, der Höhe h und dem x. Das x stellt dabei die halbe Diagonale der Grundfläche dar, also \( x = \frac{d}{2} = \sqrt{2} · \frac{a}{2} \). Quadriert man jetzt x, wie es der Pythagoras verlangt, so erhält man \( x^2 = ( \sqrt{2} · \frac{a}{2} )^2 = \frac{a^2}{2} \).
Damit ergibt sich die Formel:
\( s = \sqrt{h^2 + x^2} = \sqrt{h^2 + \frac{a^2}{2} } \)
Grundfläche G
Die Grundfläche entspricht der eines Quadrates und ist mit G = a² anzugeben.
Mantelfläche M
Wir haben vier gleichschenklige Dreiecke und können diese mit M = 2·a·ha bestimmen, wobei ein Dreieck den Flächeninhalt ADreieck = 1/2·a·ha besitzt.
Oberfläche O
Die Oberfläche setzt sich wie gewohnt aus der Grundfläche und der Mantelfläche zusammen. Damit haben wir O = G + M = a² + 2·a·ha.
Volumen V
Das Volumen einer Pyramide ergibt sich zu V = \( \frac{1}{3} \)·G·h. Den Faktor \( \frac{1}{3} \) kann man leicht anhand eines Würfels veranschaulichen. Wir haben dabei einen Würfel mit der Kantenlänge a, also dem Volumen VW = a³. In diesen passen 6 Pyramiden, deren Spitzen sich in der Mitte treffen.

Wenn man sich jetzt nur den halben Würfel vorstellt, so hat man ein Volumen von VW/2 = 1/2·a·a·a. Schaut man nochmals in der Grafik nach, so ist klar, dass die Höhe einer Pyramide mit \( h = \frac{1}{2}·a \) angegeben werden kann. Betrachten wir weiterhin den halben Würfel, so wissen wir, dass VW/2 = 3·V sein muss, denn im halben Würfel haben wir nicht mehr sechs, sondern drei Pyramiden. So ergibt sich für die Pyramide V = \( \frac{1}{3} \)·VW/2 = \( \frac{1}{3} · \frac{1}{2} \)·a·a·a = \( \frac{1}{3} \)·h·a·a = \( \frac{1}{3} \)·G·h.

Winkel in Pyramiden
In der Pyramide finden wir zwei Winkel, wie in folgender Abbildung dargstellt. Sie lassen sich bei gegebenen Seiten mit dem Kosinussatz berechnen.