Lektion F03: Lineare Funktionen in Normalform
Lineare Funktion in Normalform - Funktionsgleichung
Funktionsgleichung in Normalform f(x) = m·x + n, Lineare Gleichung, Schnittpunkt mit y-Achse, Steigung und Steigungsdreieck
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
F03-2 Lineare Funktion in Normalform - Gleichung aus 2 PunktenFunktion aus 2 Punkten ermitteln und Funktionsgleichung aufstellen (Schnittpunkt mit y-Achse und Steigung), Achsenschnittpunkte ermitteln
-
F03-3 Lineare Funktion in Normalform - Konstante Funktion, NullstellenFunktionsgleichung und konstante Funktion, Nullstelle und Nullstellenberechnung, senkrechter Funktionsgraph
-
F03-4 Gerade ins Koordinatensystem einzeichnen (Steigung)Wie zeichnet man eine Gerade in ein Koordinatensystem ein? Man hat eine Funktionsgleichung und soll diese als Graph zeichnen. Wir klären auf, wie man vorgeht und welche Verfahren es gibt.
-
F03-5 Liegt der Punkt auf dem Graphen (rechnerisch bestimmen)Ob ein Punkt auf einem Graphen liegt, lässt sich schnell überprüfen. In diesem kurzen Video zeigen wir, wie man das rechnerisch bestimmen kann.
Das war wirklich viel Neues in den Videos. Nutzt als nächstes die Lernprogramme, um euer Wissen zu testen.
Die Steigung eines linearen Graphen wird allgemein meist mit „m“ bezeichnet (einer sogenannten Variablen). Das „m“ steht vor dem x. Die Steigung ergibt sich aus dem Verhältnis von Höhe zu Breite. Eine Steigung kann positiv, negativ, null oder sogar „nicht definiert“ sein.
Im Folgenden könnt ihr die Lernprogramme nutzen, um euer Wissen zu den linearen Funktionen zu testen:
-
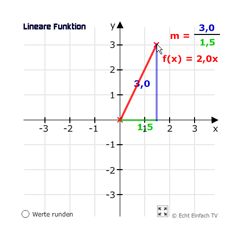Steigung eines linearen GraphenBewegt die Maus und seht die Abstände für Breite (grün) und Höhe (blau) und die sich ergebende Steigung m (der Wert, der vor dem x steht). -
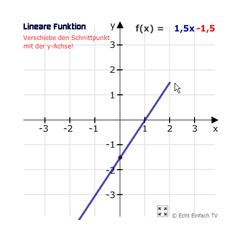Steigung und Schnittpunkt mit y-AchseZuerst die Steigung wählen (mit Mausklick bestätigen) und danach die Höhe auf der y-Achse einstellen. Die Normalform wird dabei angezeigt. -
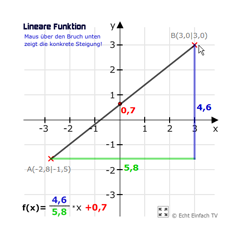Lineare Funktion in NormalformHier könnt ihr euch die Normalform einer Funktion: f(x) = m·x + n erstellen, indem ihr zwei Punkte A und B setzt. -
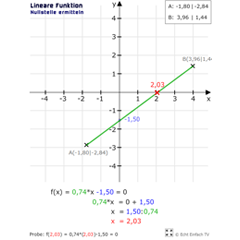Nullstellen des linearen GraphenMit diesem Programm könnt ihr zwei Punkte A und B setzen und erhaltet die Funktionsgleichung sowie die schrittweise Berechnung der Nullstelle angezeigt. -
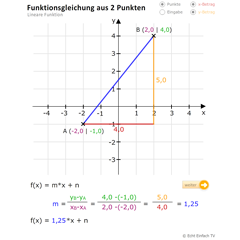Lineare Funktion aus 2 PunktenDieses Programm berechnet aus zwei Punkten die Funktionsgleichung einer linearen Funktion. Gebt auch eigene Punkte ein. Zusätzlich wird euch der Rechenweg angezeigt.
Hier findest du 2 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 2 Lernchecks, mit denen du dein Wissen testen kannst.
Häufige Fragen:
- Funktionsgleichung anhand 2 gegebener Punkte
- Graph der Funktion f(x) = x/2 + 2
- Gerade ins Koordinatensystem einzeichnen (Steigung)?
- Funktionsgleichung aus 2 Punkten ermitteln?
- Welche Steigung hat eine Gerade, wenn 2 Punkten übereinander liegen?
- Liegt der Punkt auf dem Graphen (rechnerisch bestimmen)?
- Steigung einer Strecke aus 2 Punkten ermitteln
- Lineare Funktionen: Nullstellen berechnen?
Finde weitere Fragen und Antworten in der Mathelounge.