Lektion G10: Primzahlen, Primfaktorzerlegung
Primzahlen sind die eigentlichen Königinnen unter den Zahlen! Warum? Weshalb? Ganz einfach: Jede natürliche Zahl besteht aus Primzahlen, man kann sie zerlegen (nur die "1" ist per Definition ausgeschlossen). Doch seht selbst in dem folgenden Video.
Weitere Videos für Kunden:
-
G10-1 Primzahlen und PrimfaktorzerlegungPrimzahlen (Natürliche Zahlen, die nur Teiler 1 und sich selbst haben) und die Primfaktorzerlegung (Darstellung einer Zahl als Multiplikation von Primzahlen). Methode zum Finden von Primzahlen.
Hier könnt ihr feststellen, ob eine Zahl Primzahl ist oder nicht (sozusagen ein „Primzahl-Test“):
Mit dem folgenden Programm könnt ihr die Primzahlen bis 1000 (größte Primzahl bis 1000 ist die 997) der Länge nach ablaufen. Verwendet die Pfeile oder scrollt einfach mit der Maus:
-
PrimfaktorzerlegungWählt eine beliebige Zahl aus und erfahrt, ob es eine Primzahl ist. Falls nicht, so erfolgt die Zerlegung in ihre Primfaktoren. -
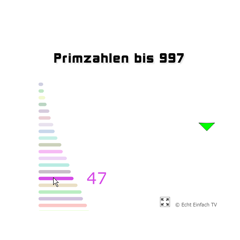Primzahlen 2 bis 997Die Primzahlen 2 bis 997 grafisch über ihre Längen dargestellt. -
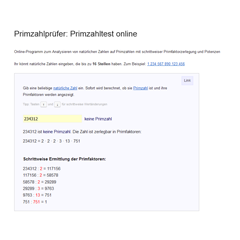PrimzahlprüferMit dem Primzahl-Prüfer online könnt ihr eine Zahl prüfen, ob sie Primzahl ist. Zusätzlich werden euch die Primfaktoren der Zahl angezeigt.
Hier findest du 4 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 3 Lernchecks, mit denen du dein Wissen testen kannst.
Häufige Fragen:
- Wie kann man sich Primzahlen bis Tausend einfach merken?
- Schreibe eine Gleichung auf, die 64 als Produkt von Primzahlen zeigt
- Primzahlen zwischen 1 und n deren Quersumme wiederum eine Primzahl ist
Finde weitere Fragen und Antworten in der Mathelounge.