Lektion TRI08: Trigonometrische Gleichungen
In dieser Lektion schauen wir uns an, wie wir trigonometrische Gleichungen am besten lösen können. Wir hatten bereits zuvor bei den trigonometrischen Funktionen gesehen, wie wir die allgemeinen Funktionsgleichungen verändern können und damit den Verlauf der Graphen. Nun werden wir unter anderem die Nullstellen dieser Graphen berechnen.
Trigonometrische Gleichung - Einführung
Einführung zu Gleichungen und Lösungsmöglichkeiten (1 Lösung, mehrere Lösungen, keine Lösung). Was ist das Intervall und wie beeinflusst es die Lösungsmenge bei den Trigonometrischen Gleichungen. Wie ist die Lösung im Bogenmaß anzugeben.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
TRI08-2 Trigonometrische Gleichung - Zweite Lösung per IdentitätDie Gleichung sin(x)=0,5 hat 2 Lösungen im Intervall [0°, 360°]. Darstellung der 2. Lösung am Einheitskreis mittels Identität sin(x) = sin(180°-x). Wir lernen den Periodizitätssummand kennen. Lösung am Sinusgraphen, Umrechnung der Lösung ins Bogenmaß.
-
TRI08-3 Trigonometrische Gleichung - cos(x)=-0,5 und sin(2·x)=0,5 lösenWir lösen die Gleichung cos(x)=-0,5. Darstellung am Einheitskreis. 2. Lösung mit Hilfe der Identität cos(x) = cos(-x). Periodizitätssummand bei Kosinus. Lösung der Aufgabe: sin(2·x)=0,5. Wie verändert der Faktor vor x die Lösung + Periode. Darstellung am Funktionsgraphen.
-
TRI08-4 Trigonometrische Gleichung - Nullstellen des SinusgraphenWir untersuchen sin(x), sin(2x), sin(x+10°), sin(x-90°) und sin(2·x-90°). Auswirkungen auf die Nullstelle des Sinusgraphen. Herleitung der allgemeinen Lösungsformel x = -c/b + k·180/b für alle Nullstellen von sin(b·x)+c = 0.
-
TRI08-5 Trigonometrische Gleichung - Lösen von SinusgleichungenNullstellen bei a·sin(b·x+c)+d=0. Lösung der Gleichung sin(2x+30°)-0,5=0. Berechnung der Periode und Ermittlung der 2. Nullstelle mittels Sinusidentität unter Berücksichtigung der veränderten Sinusgleichung.
-
TRI08-6 Trigonometrische Gleichung - KosinusgleichungenWir lösen die Kosinusgleichung cos(2x-90°)+0,5=0. Ermittlung der zweiten Lösung über Kosinusidentität.
-
TRI08-7 Trigonometrische Gleichung - TangensgleichungenWir lösen die Tangensgleichung: 0,3·tan(1,5x-90°)+0,3=0. Periode bei Tangens mit 180°/b.
-
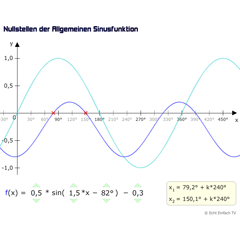Sinusfunktion NullstellenDieses Programm berechnet uns die Nullstellen der allgemeinen Sinusfunktion a·sin(b·x+c)+d und zeigt sie im Koordinatensystem an. Verändert ihr die Werte, verändert sich der Graph. -
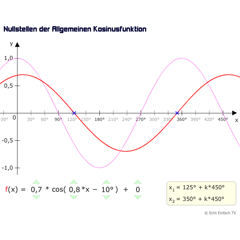Kosinusfunktion NullstellenDieses Programm berechnet uns die Nullstellen der allgemeinen Kosinusfunktion a·cos(b·x+c)+d und zeigt sie im Koordinatensystem an. -
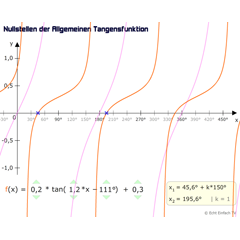Tangensfunktion NullstellenDieses Programm berechnet uns die Nullstellen der allgemeinen Tangensfunktion a·tan(b·x+c)+d und zeigt sie im Koordinatensystem an.
Hier findest du 2 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 1 Lerncheck, mit dem du dein Wissen testen kannst.
Artikel im Wiki:
- Trigonometrische Gleichungen - Einführung
- Lösung von sin(x) = 0,5 per Identität
- Lösen der trigonometrischen Gleichungen: cos(x) = -0,5
- Lösen der trigonometrischen Gleichungen: sin(2·x) = 0,5
- Nullstellen des Sinusgraphen berechnen
- Lösung zur Sinusgleichung sin(3·x - 90°)
- Lösen von Sinusgleichungen der Form sin(b·x + c) + d = 0
- Sinusgleichung ohne Lösung
- Kosinusgleichungen lösen
- Lösen der Kosinusgleichung 1·cos(2·x-90°) + 0,5
- Tangensgleichung lösen
Häufige Fragen:
- Zweite Nullstelle bei allgemeiner Sinusfunktion über Identität bestimmen?
- Nullstellen berechnen für trigonometrische Funktion f(x) = cos(x) + 2·cos(x)·sin(x)?
- Korrekte Schreibweise für den Wertebereich in Mathe (Sinus)?
- Entspricht √2·sin²(x) = 2·sin(x)?
- Trigonometrische Gleichung lösen: sin(2x + 2) = 1 in [-4,4]
- Trigonomentrische Funktion Schnittpunkt für sin(x) = sin(2x) ermitteln
- Zeichne die Graphen der folgenden Funktionen 0 ≤ x ≤ 2π
Finde weitere Fragen und Antworten in der Mathelounge.