Lektion TRI09: Additionstheoreme
Nachdem wir die trigonometrischen Gleichungen kennengelernt haben und sicherer im Umgang mit deren Umformungen sind, können wir uns die sogenannten Additionstheoreme („Additionssätze“) für Sinus, Kosinus und Tangens anschauen.
Additionstheoreme - Verständliche Herleitung für Sinus
In diesem Video zeigen wir die grafische Herleitung des Additionstheorems für Sinus mit sin(α+β) = sin(α)·cos(β)+cos(α)·sin(β) sowie die Anwendung der Additionstheoreme zum Nachweis von trigonometrischen Identitäten.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
TRI09-2 Additionstheoreme - Zum Nachweis von Sinuswerten über 90°Wir zeigen, wie das Sinus-Additionstheorem zum rechnerischen Nachweis von Sinuswerten für Winkel größer 90° genutzt werden kann.
-
TRI09-3 Additionstheoreme - Verständliche Herleitung für KosinusVollständige Herleitung des Additionstheorems für Kosinus: cos(α+β) = cos(α)·cos(β)+sin(α)·sin(β)
-
TRI09-4 Additionstheoreme - Herleitung für TangensWir zeigen, wie sich das Additionstheorem für Tangens ergibt mit: tan(α + β) = ( tan(α) + tan(β) ) / ( 1 - tan(α)·tan(β) ). Danach nutzen wir das Additionstheorem, um Tangenswerte für Winkel größer 90° zu berechnen.
-
TRI09-5 Additionstheoreme - Weitere AdditionstheoremeWas passiert, wenn wir statt sin(α + β) ein sin(α - β) haben? Es ergeben sich neue Additionstheoreme. Wir zeigen, welche das sind für sin(α - β), cos(α - β) und tan(α - β) inklusive Herleitung.
-
TRI09-6 Additionstheoreme - Herleitung DoppelwinkelfunktionenDie Doppelwinkelfunktionen sind ein Spezialfall der Additionstheoreme, hier wird der Sinus/Kosinus/Tangens vom doppelten Winkel betrachtet. Welche neuen Formeln sich ergeben, lernen wir in diesem Video. Abschließend lösen wir noch einige Aufgaben mit Hilfe der Additionstheoreme.
-
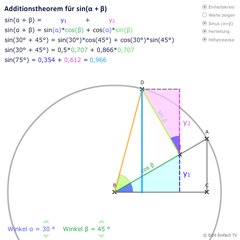Additionstheorem für SinusHier wird euch das Additionstheorem sin(a+b) = sin(a)·cos(b) + cos(a)·sin(b) grafisch hergeleitet, das wir benutzen, um den Sinuswert des Gesamtwinkels zu berechnen. -
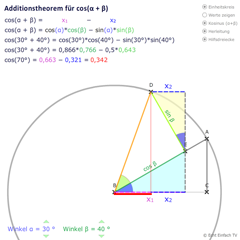Additionstheorem für KosinusHier wird euch das Additionstheorem cos(a+b) = cos(a)·cos(b) + sin(a)·sin(b) grafisch hergeleitet, das wir benutzen, um den Kosinuswert des Gesamtwinkels zu berechnen.
Hier findest du 2 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 2 Lernchecks, mit denen du dein Wissen testen kannst.
Artikel im Wiki:
Häufige Fragen:
- Trigonometrie: Wieso ist sin(70°) = cos(20°)?
- Für welche Werte gilt die Ungleichung cos(α+β) ≠ cos(α) + cos(β) nicht?
- Worin besteht der Unterschied zwischen Additionstheoremen und Doppelwinkelfunktionen?
- Warum ist sin²x - cos²x = -cos(2x)?
- Additionstheoreme: sin(x+pi/2)=cos(x)
- Berechnen Sie cos(15°) aus cos(30°) und sin(30°) mit Hilfe der Addiontstheoreme für Kosinus und Sinus.
Finde weitere Fragen und Antworten in der Mathelounge.