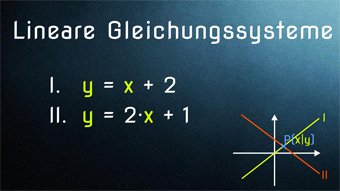Das Einsetzungsverfahren ähnelt dem Gleichsetzungsverfahren, jedoch stellen wir nur eine Gleichung nach y um (die zweite Gleichung lässt man unverändert):
I. y = (…)
II. y + (…) = (…)
Dann dürfen wir den Term für y aus Gleichung I, also y = (…) in die II. Gleichung einsetzen. Wir ersetzen also y von Gleichung II mit dem Wert von y aus Gleichung I.
II. y + (…) = (…)
II'. (…) + (…) = (…)
Schließlich enthält die neu entstehende Gleichung II' keine y mehr, sondern nur noch Unbekannte x und lässt sich lösen.
Anstatt nach y kann man nach jeder beliebigen Variablen umstellen. Das funktioniert entsprechend.