f(x) = sin(x) | Kehrwert bilden
g(x) = \( \frac{1}{ \textcolor{#00F}{\sin(x)} } \)
Die Kehrwertfunktion nennen wir „Kosekans“ (oder Kosekansfunktion). Abkürzung: csc(x)
Wenn wir sie am Dreieck verstehen wollen, setzen wir Gegenkathete und Hypotenuse ein:
f(x) = sin(x) = \( \frac{GK}{HY} \) | Kehrwert bilden
g(x) = \( \frac{1}{\frac{GK}{HY}} = \frac{HY}{GK}\)
Wir fragen mit dem Kehrwert jetzt also nicht mehr wie beim Sinus, wie lange ist die Gegenkathete im Verhältnis zur Hypotenuse, wir fragen jetzt vielmehr wie lang ist die Hypotenuse im Vergleich zur Gegenkathete.
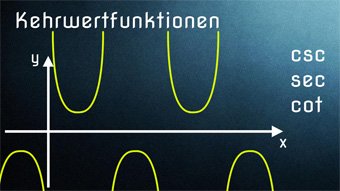
Dabei können die Werte für Kosekans alle reellen Zahlen annehmen, nur Zahlenwerte zwischen -1 und 1 sind nicht möglich. Dies kann man übrigens auch gut am Graphen erkennen:
~plot~ 1/sin(x);noinput ~plot~
Noch ein Beispiel mit Sinus und Kosekans am Dreieck: Mit sin(30°) erhalten wir 0,5. Das heißt in einem Dreieck wird die Gegenkathete halb so lang sein wie die Hypotenuse. Berechnen wir jetzt den Kosekans von 30°, also csc(30°) = 2. Das heißt, die Hypotenuse ergibt sich aus 2 mal der Gegenkathete.