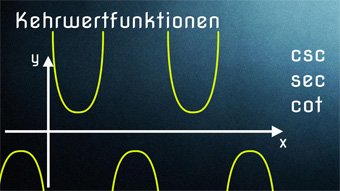
Hier ist es dem Sinus sehr ähnlich, denn der Kosinus ist ja nichts weiter als der um 90° verschobene Sinus.
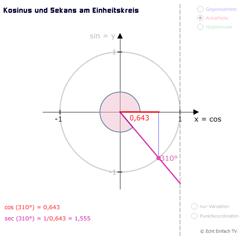
In der Abbildung ist die Länge der lila Linie der Wert für Sekans:

In diesem Beispiel ist sec(60°) = 2.
Der Sekans lässt sich übrigens an der Strecke ablesen, weil sich mit ihr ein rechtwinkliges Dreieck ergibt:

Dort ist die Ankathete bzw. Breite immer 1 (siehe gestrichelte senkrechte Linie bei x = 1), egal welchen Winkel wir einstellen (im 1. und 4. Quadrant).
Das heißt bei:
\( \cos(α) = \frac{AK}{HY} \)
können wir AK = 1 einsetzen und erhalten:
\( \cos(α) = \frac{1}{HY} \)
\( HY = \frac{1}{\cos(α)} \)
Und wir wissen, dass \( \frac{1}{\cos(α)} \) die Kehrwertfunktion von Kosinus ist, also Sekans. Daher entspricht die Länge der Hypotenuse dem Wert für Sekans: \( HY = \frac{1}{\cos(α)} = \sec(x) \)