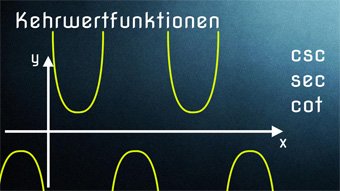
Der blaue Kotangesgraph ergibt sich, indem wir 1 durch jeden Tangenswert rechnen. Im Gegensatz zum Kosekans und Sekans kann der Graph der Kotangensfunktion alle beliebigen Werte annehmen.
Er hat aber auch Definitionslücken, wo Tangens 0 ist. Also zum Beispiel bei 0° oder bei 180°. Die Periode von 0° bis 180°, dann von 180° bis 360° etc.
~plot~ cot(x);noinput ~plot~
Auch diesen Graphen können wir strecken, stauchen, nach rechts und links verschieben und nach oben und unten verschieben. Beispiel:
f(x) = 2·cot(0,25x-π)+1
~plot~ 2*cot(0.25x-pi)+1;[[15]];noinput ~plot~
Beispielaufgabe: Schnittpunkt von Tangensfunktion mit Kotangensfunktion
Die Aufgabe soll lauten:
Berechne den Schnittpunkt der beiden Funktionen:
f(x) = cot(x - 30°)
k(x) = tan(x - 30°)
im Intervall Intervall 0° bis 90°.
Um einen Schnittpunkt zu berechnen, müssen wir grundsätzlich die beiden Gleichungen gleichsetzen.
f(x) = k(x)
cot(x - 30°) = tan(x - 30°)
Nun machen wir es uns einfacher, indem wir Kotangens in Tangens umwandeln:
\( \frac{1}{ \tan(x - 30°) } \) = tan(x - 30°)
Dann können wir umformen:
\( \frac{1}{ \tan(x - 30°) } \) = tan(x - 30°) | · tan(x - 30°)
1 = tan(x - 30°) · tan(x - 30°)
1 = tan2(x - 30°) | ±√
\( \pm \sqrt{1} \) = \( \sqrt{ \tan^2(x - 30°) } \)
±1 = tan(x - 30°)
Berechnen wir den Wert mit dem Arkustangens:
±1 = tan(x - 30°) | tan-1()
tan-1(±1) = tan-1(tan(x - 30°))
±45° = x - 30°
x1 = 75°
x2 = -15°
Lösung x2 ist nicht im Intervall 0° bis 90° und wird vernachlässigt. Wir haben nur die Lösung: x1 = 75°
Probe:
f(x) = cot(x - 30°) → f(75°) = cot(75° - 30°) = cot(45°) = 1
k(x) = tan(x - 30°) → tan(75° - 30°) = tan(45°) = 1
Beide haben den gemeinsamen Punkt P(75° | 1) und schneiden sich dadurch.
Hier die Graphen:
~plot~ tan(x-30/180*pi);cot(x-30/180*pi);x=75/180*pi;[[-3|4|-4|4]];noinput ~plot~
Unsere Lösung ist korrekt.