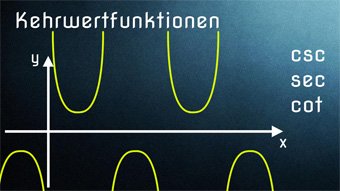
Wir kommen mit folgenden Schritten zur Umkehrfunktion der allgemeinen Sinusfunktion:
\( a·\sin(b·x + c) + d = y \\ a·sin(b·x + c) = y - d \\ sin(b·x + c) = \frac{y - d}{a} \\ b·x + c = sin^{-1}( \frac{y - d}{a} ) \\ b·x = sin^{-1}( \frac{y - d}{a} ) - c \\ x = \frac{ sin^{-1}( \frac{y - d}{a} ) - c } { b } \\ f^{-1} = \frac{ \sin^{-1}( \frac{y - d}{a} ) - c } { b } \)
Das f-1 steht für die Umkehrfunktion.