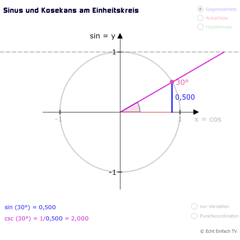
Kosekans (also die Kehrwertfunktion von Sinus) können wir auch direkt am Einheitskreis ablesen. Die Länge der lila Linie gibt den Wert für Kosekans an:

sin(30°) = 0,5
csc(30°) = \( \frac{1}{0,5} = 2 \)
Kosekans lässt sich an dieser Strecke ablesen, weil sich mit ihr ein rechtwinkliges Dreieck wie folgt ergibt:

Die Gegenkathete bzw. Höhe ist immer 1, siehe gestrichelte Linie bei y = 1, egal welchen Winkel wir einstellen (zwischen 0° und 180°).
Das heißt bei:
\( \sin(α) = \frac{GK}{HY} \)
können wir GK = 1 einsetzen und erhalten:
\( \sin(α) = \frac{1}{HY} \)
\( HY = \frac{1}{\sin(α)} \)
Und wir wissen, dass \( \frac{1}{\sin(α)} \) die Kehrwertfunktion von Sinus ist, also Kosekans. Daher entspricht die Länge der Hypotenuse dem Wert für Kosekans: \( HY = \frac{1}{\sin(α)} = \csc(x) \)
Am Einheitskreis erkennt man auch, dass die Werte nicht zwischen -1 und 1 liegen können, da die Hypotenuse nie kürzer als die Gegenkathete sein kann.
Aufzupassen ist bei 0°, denn csc(0°) = \( \frac{1}{\sin(0°)} \) = \( \frac{1}{0} \) = nicht definiert.
Gleiches bei 180°, denn csc(180°) = \( \frac{1}{\sin(180°)} \) = \( \frac{1}{0} \) = nicht definiert.
Zu merken ist außerdem: csc(90°) = \( \frac{1}{\sin(90°)} \) = \( \frac{1}{1} \) = 1
Wenn wir Winkel zwischen 180° und 360° haben, dann ergeben sich negative Werte für Kosekans. Beispiele:
csc(230°) = \( \frac{1}{\sin(230°)} \) = -1,3054…
csc(270°) = \( \frac{1}{\sin(270°)} \) = \( \frac{1}{-1} \) = -1
csc(320°) = \( \frac{1}{\sin(320°)} \) = -1,5557…
csc(360°) = \( \frac{1}{\sin(360°)} \) = \( \frac{1}{0} \) = nicht definiert