Hier ist die nächste Identität, es gilt:
cos(α) = sin(β)
cos(α) = sin(90° - α)
Mit der Identität sin(α) = cos(90° - α) können wir uns aus dem gegebenen Sinuswert den Kosinuswert ermitteln. Ein Beispiel:
sin(α) = cos(90° - α)
sin(60°) ≈ 0,866
sin(60°) = cos(90° - 60°)
sin(60°) = cos(30°)
0,866 ≈ cos(30°)
Wenn wir den Sinuswert von 60° kennen, in diesem Fall rund 0,866, dann wissen wir sofort, dass der Kosinus von 30° ebenfalls 0,866 ist.
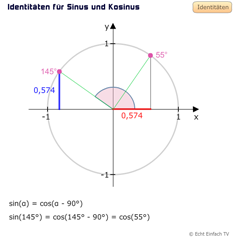
Wenn wir sin(α) und cos(90° - α) zeichnen, erkennen wir, dass der Kosinus der Sinus des Komplimentärwinkels ist. Siehe Abbildung: