Die Koordinatengleichung ist ein Spezialfall der sogenannten Kreisgleichung (x-xM)2 + (y-yM)2 = r2, die wir uns in einer späteren Lektion anschauen. Liegt der Mittelpunkt M im Koordinantenursprung ergibt sich:
(x - xM)2 + (y - yM)2 = r2
(x - 0)2 + (y - 0)2 = r2
x2 + y2 = r2
Die Koordinatengleichung lautet: x² + y² = 1.
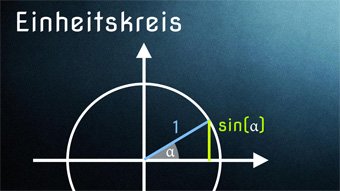
Dabei sind x und y die Koordinaten unseres auf der Kreislinie des Einheitskreises liegenden Punktes P.
Die Gleichung entsteht, wenn wir das zuvor kennengelernte Wissen kombinierten. Zum einen das Wissen, dass die x-Koordinate des Punktes P (auf dem Einheitskreis) dem Sinuswert und die y-Koordinate des Punktes P dem Kosinuswert entspricht. Zum anderen den bereits gelernten trigonometrischen Pythagoras mit: sin2(β) + cos2(β) = 1
P( x | y ) → P( cos(β) | sin(β) )
sin2(β) + cos2(β) = 1 | sin(β) = y
y2 + cos2(β) = 1 | cos(β) = x
y2 + x2 = 1
x2 + y2 = 1