Die sogenannten Identitäten helfen uns bei verschiedenen Sachverhalten. Mit ihrer Hilfe können wir Sinus in Kosinus überführen, alle Sinus-/Kosinuswerte auf Winkel von 0° bis 90° zurückführen, rechnerisch weitere Winkel bestimmen, schwierige trigonometrische Gleichungen vereinfachen und auflösen.
Es gibt sehr viele Identitäten, wir lernen hier die grundlegenden Identitäten kennen. Hier eine Übersicht:
- sin(α) = cos(90° - α)
- cos(α) = sin(90° - α)
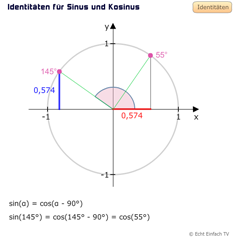
- sin(α) = cos(α - 90°)
- sin(α) = -sin(-α)
- cos(α) = cos(-α)
- sin(90° + α) = sin(90° - α)
- cos(90° + α) = -cos(90° - α)
- sin(α) = sin(α + 360°) und cos(α) = cos(α + 360°)
Das Programm Einheitskreis: Identitäten für Sinus und Kosinus zeigt die vorgenannten und weitere Identitäten auf. Dort sehen wir animiert/interaktiv, wie sich die Identitäten verhalten.