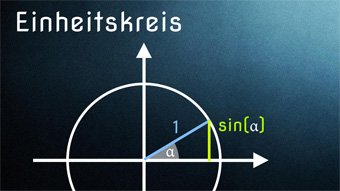
Es gibt Sinus- und Kosinuswerte, die man kennen muss. Hierzu stellt man sich einfach den Einheitskreis vor, zeichnet in Gedanken das Dreieck zum Winkel ein und liest den Wert an Gegenkathete (Sinus) oder Ankathete (Kosinus) ab.
Wichtige Sinuswerte
sin(0°) = 0
sin(90°) = 1
sin(180°) = 0
sin(270°) = -1
sin(360°) = 0
Wichtige Kosinuswerte
cos(0°) = 1
cos(90°) = 0
cos(180°) = -1
cos(270°) = 0
cos(360°) = 1
Statt Gradzahlen kann man auch das Bogenmaß verwenden.
Die gleiche Aufstellung mit dem Bogenmaß (die Einheit rad schreibt man meist nicht mit, also statt 0 rad schreibt man einfach 0) lautet:
Wichtige Sinuswerte (Winkel in Gradmaß und Bogenmaß)
sin(0°) = sin(0) = 0
sin(90°) = sin(1⁄2·π) = 1
sin(180°) = sin(1·π) = 0
sin(270°) = sin(3⁄2·π) = -1
sin(360°) = sin(2·π) = 0
Wichtige Kosinuswerte (Winkel in Gradmaß und Bogenmaß)
cos(0°) = cos(0) = 1
cos(90°) = cos(1⁄2·π) = 0
cos(180°) = cos(1·π) = -1
cos(270°) = cos(3⁄2·π) = 0
cos(360°) = cos(2·π) = 1
Tabelle zu besonderen Werten für Sinus und Kosinus (Bogenmaß)
| α im Gradmaß | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| α im Bogenmaß | 0 | \( \frac{ \pi }{6} \) | \( \frac{ \pi }{4} \) | \( \frac{ \pi }{3} \) | \( \frac{ \pi }{2} \) |
| sin(α) | 0 | \( \frac{1}{2} \) | \( \frac{1}{2}·\sqrt{2} \) | \( \frac{1}{2}·\sqrt{3} \) | 1 |
| Merkhilfe für sin(α) | \( \frac{1}{2}·\sqrt{0} \) | \( \frac{1}{2}·\sqrt{1} \) | \( \frac{1}{2}·\sqrt{2} \) | \( \frac{1}{2}·\sqrt{3} \) | \( \frac{1}{2}·\sqrt{4} \) |
| cos(α) | 1 | \( \frac{1}{2}·\sqrt{3} \) | \( \frac{1}{2}·\sqrt{2} \) | \( \frac{1}{2} \) | 0 |
| tan(α) | 0 | \( \frac{1}{3}·\sqrt{3} \) | 1 | \( \sqrt{3} \) | nicht definiert |