Herleitung des Trigonometrischen Pythagoras
Erinnern wir uns zuerst an den Satz des Pythagoras mit a² + b² = c². Wenn wir die Hypotenuse mit c = 1 festlegen, dann ergibt sich bei Anwendung am rechtwinkligen Dreieck:
a² + b² = c² | c = 1
a² + b² = 1²
a² + b² = 1
Wir wissen, dass bei einer Hypotenuse mit der Länge 1 die Gegenkathete dem Sinuswert entspricht und die Ankathete dem Kosinuswert. Also in der Abbildung b ist der Sinuswert und a ist der Kosinuswert:
\( a = \cos( \beta ) = \frac{AK}{HY} = \frac{a}{1} \\ b = \sin( \beta ) = \frac{GK}{HY} = \frac{b}{1} \)
Somit können wir einsetzen:
a2 + b2 = 1 | a = cos(β) und b = sin(β)
(cos(β))2 + (sin(β))2 = 1
Das Quadratzeichen schreibt man direkt an das sin bzw. cos, wir notieren also:
Die Formel für den trigonometrischen Pythagoras lautet:
cos²(β) + sin²(β) = 1
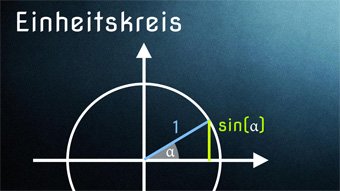
Abbildung: Trigonometrischer Pythagoras
Die folgende Abbildung stellt den trigonometrischen Pythagoras am Einheitskreis dar:

Alternative Herleitung zum trigonometrischen Pythagoras
Eine schnellere Herleitung ist algebraisch (also auf rechnerischem Weg), ausgehend vom Satz des Pythagoras:
a2 + b2 = c2 | :c2
a2:c2 + b2:c2 = c2:c2
\( \frac{a^2}{c^2} + \frac{b^2}{c^2} \) = 1
\( \left( \frac{a}{c} \right)^2 + \left( \frac{b}{c} \right)^2 \) = 1 | \( \frac{a}{c} \) = cos(β)
(cos(β))2 + \( \left( \frac{b}{c} \right)^2 \) = 1 | \( \frac{b}{c} \) = sin(β)
(cos(β))2 + (sin(β))2 = 1
cos2(β) + sin2(β) = 1
sin2(β) + cos2(β) = 1
Hieraus ergibt sich auch ein neuer Zusammenhang:
sin2(β) + cos2(β) = 1
I. sin2(β) = 1 - cos2(β)
II. cos2(β) = 1 - sin2(β)
Beispielaufgabe Trigonometrischer Pythagoras
Verwenden wir die Formel, um eine Gleichung zu lösen:
cos2(13°) + sin2(13°) = x
Jetzt wissen wir, dass cos2(β) + sin2(β) = 1 ist, damit lässt sich sofort lösen:
x = cos2(13°) + sin2(13°)
x = 1
Interpretieren wir den trigonometrischen Pythagoras als Funktionsgleichung und zeichnen ihn als Graph, so erhalten wir:
~plot~ sin(x)^2+cos(x)^2;sin(x)^2;cos(x)^2;[[-3|3|-2|2.5]];noinput ~plot~
Der blaue Funktionsgraph hat immer den y-Wert y = 1.
Die geschwungenen Graphen für Sinus und Kosinus werden wir bei den Trigonometrischen Funktionen ausführlich erklären.